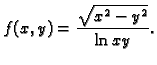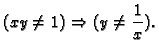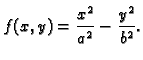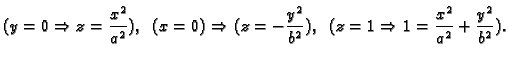



Next: Neprekidnost i limes
Up: Diferencijalni račun
Previous: Diferencijalni račun
Contents
Index
Subsections
Podsjetimo se
Domena funkcije igra važnu ulogu u proučavanju funkcije. Kad se
radilo o funkciji jedne varijable, ograničili smo se na intervale i
segmente. Domene funkcija više varijabli su skupovi u
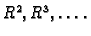 Razmotrimo zato skupove u
Razmotrimo zato skupove u 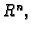 kako bismo odredili
adekvatne analogone intervalima odnosno segmentima u
kako bismo odredili
adekvatne analogone intervalima odnosno segmentima u 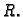
Neka su
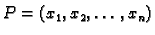 i
i
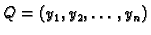 dvije točke u
dvije točke u
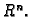 Njihova udaljenost je dana formulom
Njihova udaljenost je dana formulom
Za 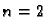 i
i 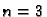 to se svodi na poznate formule za udaljenost točaka u
ravnini i prostoru. Na pr., ako je
to se svodi na poznate formule za udaljenost točaka u
ravnini i prostoru. Na pr., ako je
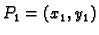 i
i
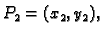 onda je
ili ako je
onda je
ili ako je
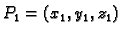 i
i
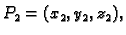 onda je
onda je
Definicija 1
Neka je
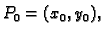
i neka je
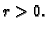
Skup
zove se
otvoreni
krug radiusa
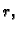
sa središtem u točki
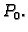
Neka je
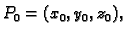 i neka je
i neka je 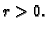 Skup
Skup
zove se
otvorena kugla radiusa
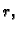
sa
središtem u točki
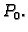
Slično, ako je
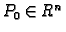 i
i 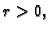 onda otvorenom kuglom u
onda otvorenom kuglom u 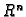 sa
središtem u
sa
središtem u 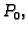 i radiusom
i radiusom 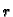 zovemo skup
zovemo skup
Skup
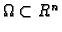 zovemo otvorenim
skupom, ako se oko svake njegove točke kao središta može opisati
otvorena kugla.
zovemo otvorenim
skupom, ako se oko svake njegove točke kao središta može opisati
otvorena kugla.
Primjer 1.1
Otvorena kugla
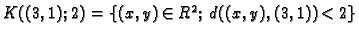
je otvoren skup.
Rješenje. Točke tog skupa su dane nejednadžbom
Ako je
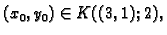
onda je
Tvrdimo da je
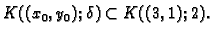
Figure 1.1:
Otvorena kugla je otvoren skup.
|
|
Zaista, neka je
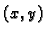
proizvoljna točka iz
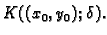
Tada je, zbog
svojstva udaljenosti (nejednakost trokuta),
Tako je
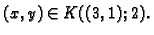
Zbog proizvoljnosti
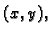
slijedi
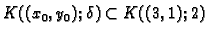
i prema tome
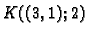
je
otvoren skup.
Definicija 2
Skup
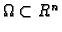
zovemo
zatvorenim skupom,
ako je njegov komplement
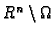
otvoren.
Definicija 3
Neka je
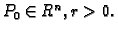
Skup
zovemo
zatvorenom kuglom u
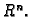
Primjer 1.2
Zatvorena kugla
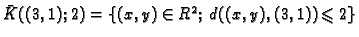
je zatvoren
skup.
Rješenje. Točke komplementa su dane nejednadžbom
tj.
Ako je
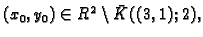
onda je
Tvrdimo da je
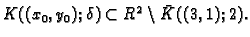
Zaista,
neka je
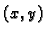
proizvoljna točka iz
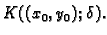
Tada je,
zbog svojstva udaljenosti,
Tako je
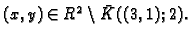
Zbog proizvoljnosti
elementa
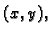
slijedi
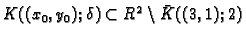
i prema
tome
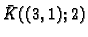
je zatvoren skup.
Figure 1.2:
Zatvorena kugla je zatvoren skup.
|
|
Zatvoreni krug smo dobili tako da smo otvorenom
krugu dodali njegov rub, kružnicu. Ako se otvorenom skupu doda samo
dio ruba, onda se dobije skup koji nije niti otvoren niti zatvoren.
Spojnica, konveksan skup, područje
Neka su
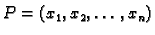 i
i
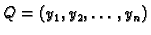 dvije
točke u
dvije
točke u 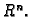 Spojnica točaka
Spojnica točaka 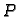 i
i 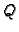 je
skup točaka na pravcu kroz
je
skup točaka na pravcu kroz 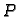 i
i 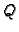 a između
a između 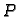 i
i 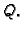 Radi
jednostavnosti razmotrimo na koji način se mogu opisati točke na
spojnici u ravnini. Neka je
Radi
jednostavnosti razmotrimo na koji način se mogu opisati točke na
spojnici u ravnini. Neka je
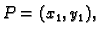
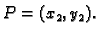 Iz slike
Iz slike
Figure 1.3:
Spojnica točaka 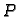 i
i 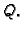
|
|
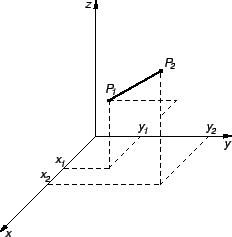
se vidi da za koordinate točke 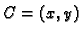 na spojnici vrijedi
na spojnici vrijedi
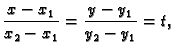
za
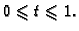
Odatle1.1
odnosno
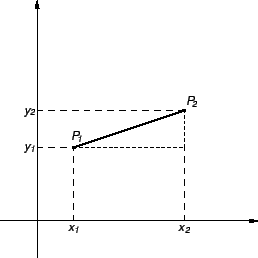
Slično, u prostoru, točke
leže na spojnici točaka
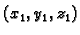 i
i
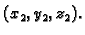 Općenito, u
Općenito, u 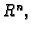 imamo da točke
leže na spojnici točaka
imamo da točke
leže na spojnici točaka
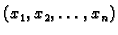 i
i
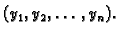
Skup
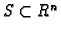 zovemo konveksnim, ako sadrži spojnicu svake dvije
svoje točke.
zovemo konveksnim, ako sadrži spojnicu svake dvije
svoje točke.
Primjer 1.3
Trokut
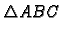
u ravnini s vrhovima
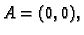
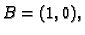
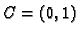
je konveksan skup.
Rješenje. Očito je
Neka je
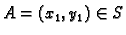
i
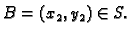
To znači
Točka na spojnici je
Za takav
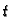
je
Dakle
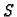
je konveksan skup.
Primjer 1.4
Skup
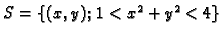
nije konveksan skup, jer točke
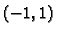
i
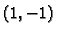
pripadaju skupu, dok točka
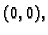
koja se nalazi na spojnici (za
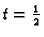
), ne pripada skupu (v. sl.
1.4).
Figure 1.4:
Skup koji nije konveksan.
|
|
Definicija 4
Otvoren skup
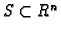
je
povezan, ako se bilo koje dvije njegove
točke mogu spojiti s konačno mnogo spojnica. Otvoren i povezan skup se zove
područje.
Primjer 1.5
Skup
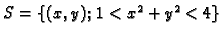
je otvoren i
povezan. Prema tome skup
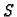
je područje.
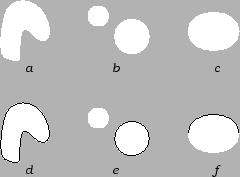
Figure 1.6:
Skupovi: a) otvoren, povezan, ali ne konveksan, b) otvoren, ali ne povezan, c) otvoren, konveksan, d) zatvoreno područje, e) niti otvoren, niti zatvoren, niti povezan, f) konveksan, niti otvoren niti zatvoren.
|
|
Definicija 5
Neka je
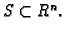
Funkcija
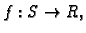
se zove
realna funkcija
od 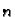 realnih varijabli
realnih varijabli.
Funkcije od dvije, tri, 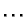 varijabli zovemo realnim funkcijama od više realnih varijabli,
ili kraće funkcijama više varijabli.
varijabli zovemo realnim funkcijama od više realnih varijabli,
ili kraće funkcijama više varijabli.
Ako je funkcija zadana formulom, onda se skup svih 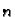 -torki, za koje
dana formula prima realne vrijednosti, zove prirodna
domena.
-torki, za koje
dana formula prima realne vrijednosti, zove prirodna
domena.
Ako je funkcija zadana samo formulom, smatrat ćemo da je domena
funkcije prirodna domena.
Kao i kod funkcija jedne realne varijable, imamo pojmove kao što su
slika funkcije, slika elementa, restrikcija funkcije, proširenje
funkcije.
Tako je slika funkcije skup
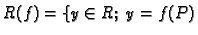
za neki
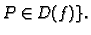
Pri tom je 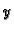 slika ili preciznije
f-slika elementa
slika ili preciznije
f-slika elementa
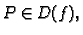 ako je
ako je
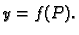
Za funkciju
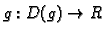 kažemo da je
restrikcija
funkcije
kažemo da je
restrikcija
funkcije
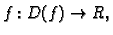 ako je
ako je
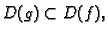 i ako je
i ako je
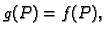 za svaki
za svaki
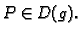
Za funkciju
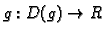 kažemo da je
proširenje
funkcije
kažemo da je
proširenje
funkcije
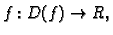 ako je
ako je
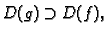 i ako je
i ako je
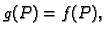 za svaki
za svaki
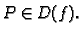
Primjer 1.6
Evo nekoliko funkcija više varijabli zadanih formulom
Primjer 1.7
Naći prirodnu domenu funkcije
Rješenje.
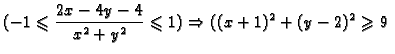
i
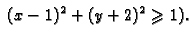
Dakle prirodna domena funkcije je osjenčani dio ravnine na slici
Grafičko prikazivanje funkcija više varijabli je ograničeno time što
nemamo metode za crtanje skupova u 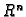 ako je
ako je 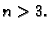
Definicija 6
Neka je
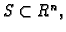
i neka je
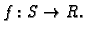 Grafom funkcije
Grafom funkcije 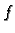
zovemo skup
Budući da je 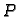
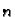 -torka realnih brojeva, a
-torka realnih brojeva, a 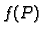 realni broj,
elementi grafa su
realni broj,
elementi grafa su 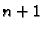 -orke, dakle
-orke, dakle
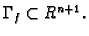
Tako je graf funkcije od dvije varijable
graf funkcije od tri varijable
Dakle, ako je dana funkcija od dvije varijable, onda njezin graf možemo
prikazati u prostoru tako da elemente domene nanosimo u ravninu 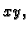 a
vrijednosti funkcije na os
a
vrijednosti funkcije na os 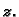 Pri tom, da bismo lakše skicirali graf,
siječemo graf koordinatnim ili nekim drugim ravninama.
Pri tom, da bismo lakše skicirali graf,
siječemo graf koordinatnim ili nekim drugim ravninama.
Primjer 1.8
Nacrtati graf funkcije
Rješenje. Nađimo presjeke s koordinatnim ravninama
Dakle to je
eliptički
paraboloid, koji postaje kružni ili
rotacijski,
ako je
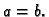
Drugi način crtanja grafa funkcija od dvije varijable jeste crtanje
nivokrivulja. Nivokrivulja je
skup točaka u domeni u kojima funkcija ima istu vrijednost. Primjer
su izohipse, izobare, 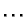 . Izohipsa 200 je krivulja koja
povezuje točke u kojima funkcija `nadmorska visina' ima vrijednost
200. Ovaj način omogućava crtanje funkcija od dvije varijable u
ravnini.
. Izohipsa 200 je krivulja koja
povezuje točke u kojima funkcija `nadmorska visina' ima vrijednost
200. Ovaj način omogućava crtanje funkcija od dvije varijable u
ravnini.
Primjer 1.9
Nacrtati graf funkcije
Rješenje. Nađimo neke nivokrivulje
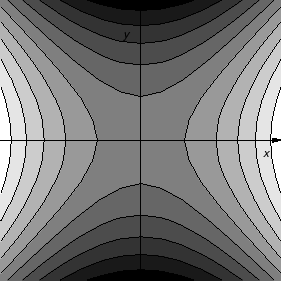
Dakle
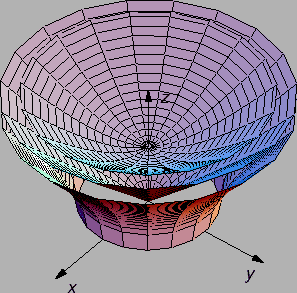
Šatirano je na taj način da je područje to svjetlije što
je na većoj visini. Kako ova ploha izgleda u prostoru vidi se na slici
4.
Kad se radi o funkcijama od tri varijable, onda skup točaka u kojima
funkcija ima istu vrijednost predstavlja neku plohu. Takva ploha se
zove nivoploha. To omogućava prikazivanje
funkcija od tri varijable u prostoru.
Primjer 1.10
Nacrtajmo nivoplohe funkcije
Rješenje.
Ova slika predstavlja samo onaj dio nivoploha koji se nalazi iznad
ravnine
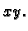
Zbog toga što u formuli varijable dolaze na kvadrat,
nivoplohe su simetrične u odnosu na koordinatne ravnine
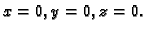
Prema tome s donje strane ravnine
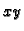
plohe se
simetrično nastavljaju. Gornja nivoploha (za
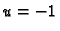
) se sastoji od dva
dijela, koji u presjeku s ravninom kroz os
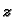
daju hiperbolu, pa se
zato zove
dvokrilni kružni
hiperboloid.
Srednja
nivoploha je stožac, koji se dodiruje vrhom s drugim stošcem ispod
ravnine
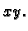
Treća nivoploha je
jednokrilni kružni
hiperboloid.
- 1.
- Što su elementi skupova
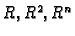 ?
?
- 2.
- Kako se definira udaljenost dvije točke u
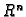 ?
?
- 3.
- Što je spojnica dviju točaka u
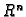 ?
?
- 4.
- Napišite koordinate proizvoljne točke
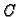 na spojnici točaka
na spojnici točaka
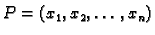 i
i
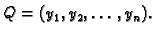
- 5.
- Definirajte otvorenu i zatvorenu kuglu u
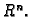
- 6.
- Definirajte otvoreni skup, zatvoreni skup, konveksan skup,
područje.
- 7.
- Što znači kad se kaže da je
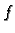 realna funkcija od više
realnih varijabli?
realna funkcija od više
realnih varijabli?
- 8.
- Što je prirodna domena funkcije više varijabli?
- 9.
- Što je graf funkcije više varijabli?
- 10.
- Kako se mogu grafički prikazivati funkcije više varijabli?
- 11.
- Što je nivokrivulja, a što nivoploha?
- 12.
- Napišite jednadžbe sljedećih ploha i skicirajte ih: kružni
(rotacijski) paraboloid, eliptički paraboloid, hiperbolički
paraboloid, jednokrilni hiperboloid, dvokrilni hiperboloid.
- 1.
- Skup
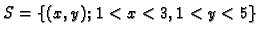 je otvoren skup.
je otvoren skup.
Rješenje. Uočimo najprije da je 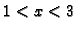 ekvivalentno s
ekvivalentno s
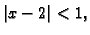 a
a 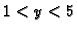 s
s 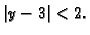
Neka je 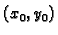 proizvoljan element iz
proizvoljan element iz
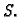 Neka je
Neka je
Očito je 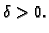 Tvrdimo da je
Tvrdimo da je
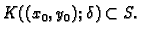 Zaista, neka je
Zaista, neka je 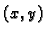 proizvoljna točka iz
proizvoljna točka iz
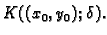 Tada je
Tako je
Tada je
Tako je 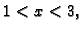 a
a 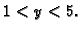 Zbog proizvoljnosti elementa
Zbog proizvoljnosti elementa 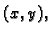 slijedi
slijedi
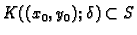 i prema tome
i prema tome 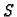 je otvoren skup.
je otvoren skup.
- 2.
- Otvoren krug
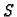 u ravnini, radiusa
u ravnini, radiusa 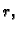 je konveksan skup.
Rješenje. Postavimo Kartezijev koordinatni sustav tako da središte kruga
bude u ishodištu. Neka su
je konveksan skup.
Rješenje. Postavimo Kartezijev koordinatni sustav tako da središte kruga
bude u ishodištu. Neka su
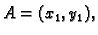 i
i
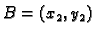 dvije
točke u
dvije
točke u 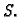 Tada postoje
Tada postoje
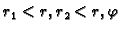 i
i 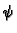 takvi da je
Neka je pri tom
takvi da je
Neka je pri tom
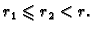
Figure 1.7:
Krug je konveksan skup.
|
|
Koordinate točke 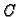 na spojnici su
Nađimo udaljenost te točke od središta kruga.
na spojnici su
Nađimo udaljenost te točke od središta kruga.
Dakle, 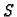 je doista konveksan skup.
je doista konveksan skup.
- 3.
- Naći prirodnu domenu funkcije
Rješenje.
Figure:
Prirodna domena funkcije
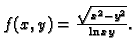
|
|
- 4.
- Nacrtati graf funkcije
Rješenje. Nađimo presjeke s koordinatnim ravninama
Ova ploha se zove hiperbolički
paraboloid.

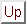



Next: Neprekidnost i limes
Up: Diferencijalni račun
Previous: Diferencijalni račun
Contents
Index
Salih Suljagic
2000-03-11
![]() Razmotrimo zato skupove u
Razmotrimo zato skupove u ![]() kako bismo odredili
adekvatne analogone intervalima odnosno segmentima u
kako bismo odredili
adekvatne analogone intervalima odnosno segmentima u ![]()
![]() i
i
![]() dvije točke u
dvije točke u
![]() Njihova udaljenost je dana formulom
Njihova udaljenost je dana formulom
![]() i neka je
i neka je ![]() Skup
Skup
![]() i
i ![]() onda otvorenom kuglom u
onda otvorenom kuglom u ![]() sa
središtem u
sa
središtem u ![]() i radiusom
i radiusom ![]() zovemo skup
zovemo skup
![]() zovemo otvorenim
skupom, ako se oko svake njegove točke kao središta može opisati
otvorena kugla.
zovemo otvorenim
skupom, ako se oko svake njegove točke kao središta može opisati
otvorena kugla.![]() i
i
![]() dvije
točke u
dvije
točke u ![]() Spojnica točaka
Spojnica točaka ![]() i
i ![]() je
skup točaka na pravcu kroz
je
skup točaka na pravcu kroz ![]() i
i ![]() a između
a između ![]() i
i ![]() Radi
jednostavnosti razmotrimo na koji način se mogu opisati točke na
spojnici u ravnini. Neka je
Radi
jednostavnosti razmotrimo na koji način se mogu opisati točke na
spojnici u ravnini. Neka je
![]()
![]() Iz slike
Iz slike
 za
za ![]() zovemo konveksnim, ako sadrži spojnicu svake dvije
svoje točke.
zovemo konveksnim, ako sadrži spojnicu svake dvije
svoje točke.
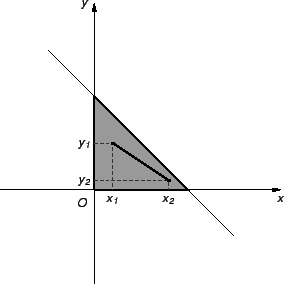
![]() varijabli zovemo realnim funkcijama od više realnih varijabli,
ili kraće funkcijama više varijabli.
varijabli zovemo realnim funkcijama od više realnih varijabli,
ili kraće funkcijama više varijabli.
![]() -torki, za koje
dana formula prima realne vrijednosti, zove prirodna
domena.
-torki, za koje
dana formula prima realne vrijednosti, zove prirodna
domena.![]() slika ili preciznije
f-slika elementa
slika ili preciznije
f-slika elementa
![]() ako je
ako je
![]()
![]() kažemo da je
restrikcija
funkcije
kažemo da je
restrikcija
funkcije
![]() ako je
ako je
![]() i ako je
i ako je
![]() za svaki
za svaki
![]()
![]() kažemo da je
proširenje
funkcije
kažemo da je
proširenje
funkcije
![]() ako je
ako je
![]() i ako je
i ako je
![]() za svaki
za svaki
![]()
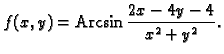
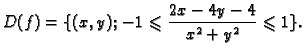
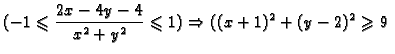 i
i 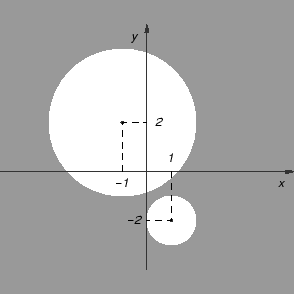
![]() ako je
ako je ![]()
![]()
![]() -torka realnih brojeva, a
-torka realnih brojeva, a ![]() realni broj,
elementi grafa su
realni broj,
elementi grafa su ![]() -orke, dakle
-orke, dakle
![]()
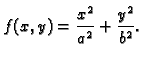
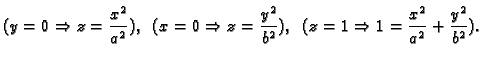
![]() . Izohipsa 200 je krivulja koja
povezuje točke u kojima funkcija `nadmorska visina' ima vrijednost
200. Ovaj način omogućava crtanje funkcija od dvije varijable u
ravnini.
. Izohipsa 200 je krivulja koja
povezuje točke u kojima funkcija `nadmorska visina' ima vrijednost
200. Ovaj način omogućava crtanje funkcija od dvije varijable u
ravnini.
![]() ekvivalentno s
ekvivalentno s
![]() a
a ![]() s
s ![]()
![]() proizvoljan element iz
proizvoljan element iz
![]() Neka je
Neka je
![]() je doista konveksan skup.
je doista konveksan skup.