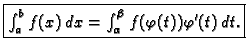
Dokaz.
![]()
Sljedeća metoda koja olakšava traženje primitivne funkcije je metoda supstitucije. Ona se temelji na sljedećem teoremu.
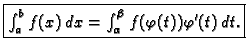
Dokaz.
![]()
Ovaj teorem vrijedi i ako ![]() nije strogo monotona, već samo po
dijelovima strogo monotona, tj. ako se
nije strogo monotona, već samo po
dijelovima strogo monotona, tj. ako se ![]() može podijeliti na konačno
mnogo segmenata takvih, da je na svakom od njih
može podijeliti na konačno
mnogo segmenata takvih, da je na svakom od njih ![]() strogo monotona.
strogo monotona.
Primjeri. 1.
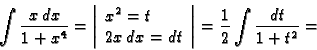
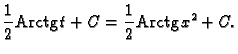
2.
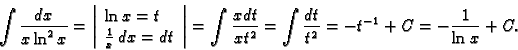
3.
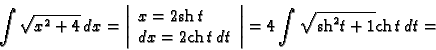
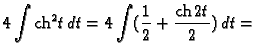
Ako je funkcija parametarski zadana
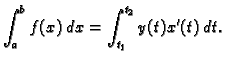
Rješenje. Parametarske
jednadžbe kružnice su
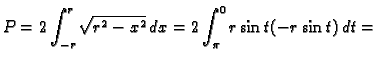
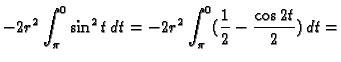
![$\displaystyle -2r^2\left[\frac{1}{2}t-\frac{\sin 2t}{4}\right]_{\pi}^0=r^2\pi.$](img3913.gif)
Ako je dana krivulja u polarnom koordinatnom sustavu u ravnini jednadžbom
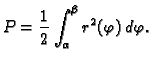
Rješenje.
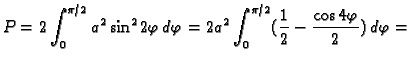
![$\displaystyle 2a^2\left[\frac{1}{2}\varphi-\frac{\sin 4\varphi}{8}\right]_0^{\pi/2}=
\frac{a^2\pi}{2}.$](img3918.gif)