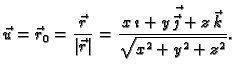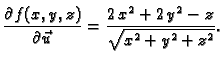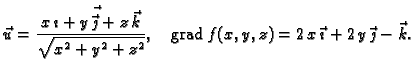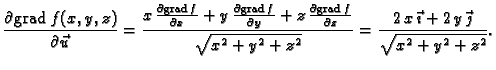



Next: Divergencija i rotacija. Specijalna
Up: Polja
Previous: Polja
Contents
Index
Subsections
Definicija 35
Neka je
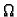
područje u
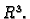
Funkciju
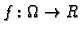
zovemo
skalarnim poljem.
Primjer 4.1
Neka materijalno tijelo
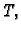
gustoće mase
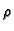
zauzima u prostoru
zatvoreno područje
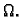
Gustoća mase, funkcija
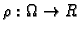
je skalarno polje.
Figure 4.1:
Gustoća mase tanke ploče. Točke u tamnijim dijelovima imaju veću gustoću.
|
|
Primjer 4.2
Temperatura
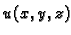
u točki
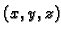
prostorije u kojoj se
nalazimo je funkcija definirana na dijelu prostora
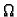
određenom ovom prostorijom, i prima vrijednosti u
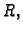
pa je
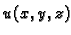
prema tome skalarno polje.
Primjer 4.3
Potencijal gravitacijskog polja točkaste mase
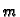
smještene u
točki
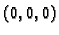
je dan formulom
gdje je
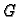
univerzalna gravitacijska konstanta. Tako je
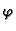
skalarno polje definirano na
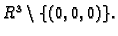
Primjer 4.4
Potencijal električnog polja točkastog naboja
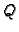
smještenog u
točki
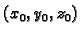
je dan formulom
gdje je
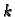
konstanta, koja ovisi o dielektričnosti sredstva
u kojem se nalazi polje. Tako je
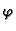
skalarno polje definirano
na
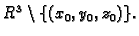
Definicija 36
Neka je
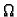
područje u
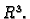
Funkciju
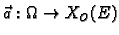
zovemo
vektorskim poljem.
Figure 4.2:
Gravitacijsko polje mase 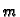 u ravnini.
u ravnini.
|
|
Primjer 4.5
Primjer vektorskog polja je gravitacijsko polje mase
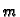
koncentrirane u točki
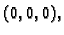
koje je dano formulom
gdje je
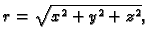
a
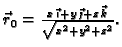
Primjer 4.6
Primjer vektorskog polja je također električno polje točkastog
naboja
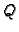
smještenog u točki
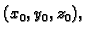
koje je dano formulom
gdje je
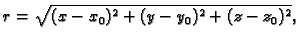
a
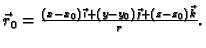
Primjer 4.7
Polje brzina gibanja nekog fluida kao na slici
4.3
Figure 4.3:
Polje brzina gibanja fluida
|
|
je također primjer vektorskog polja. Ako se slika gibanja mijenja
tokom vremena, onda brzina
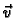
ovisi, osim o prostornim koordinatama
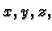
još i o vremenu
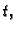
tj.
gdje je
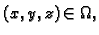
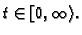
Takva polja se zovu
nestacionarna polja, za
razliku od onih koja ne ovise o vremenu i koja se zovu
stacionarna
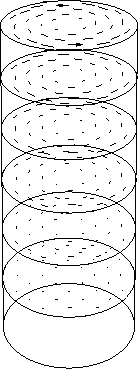
Primjer 4.8
Polje pomaka torzije
cilindra. Puni uspravni cilindar radiusa
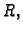
visine
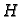
je podvrgnut
torziji. Jedna baza ostaje na miru, a kut zakreta se jednoliko
povećava do visine
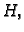
gdje iznosi
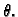
Pri tom pretpostavljamo
da se zakret svakog poprečnog presjeka vrši okomito na os
cilindra. Uočimo proizvoljnu materijalnu točku cilindra, čiji je
početni položaj
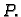
Nakon torzije ona zauzme položaj
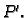
Vektor
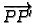
uzet s početkom u točki
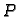
pokazuje
pomak materijalne točke prilikom torzije. Zato vektorsko polje
definirano na zatvorenom području koje na početku zauzima cilindar,
zovemo
polje pomaka. Uz pretpostavku da se radi o malom kutu
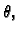
može se izvesti (v.
1) da je
Definicija 37
Neka je
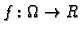
skalarno polje klase
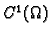
,
i neka je
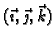
ortonormirana baza
u
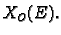
Vektorsku funkciju
zovemo
gradijentom skalarnog polja 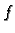
.
Gradijent funkcije 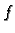 možemo shvatiti kao djelovanje diferencijalnog
operatora
možemo shvatiti kao djelovanje diferencijalnog
operatora
na funkciju 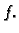 Za taj operator se, osim oznake
Za taj operator se, osim oznake
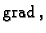 često koristi
oznaka
često koristi
oznaka 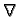 (nabla), pa se tako umjesto
(nabla), pa se tako umjesto
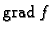 često piše
često piše
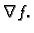
Neka je 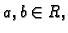 i
i 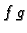 neprekidno derivabilne funkcije. Tada vrijedi
neprekidno derivabilne funkcije. Tada vrijedi
Primjer 4.9
Nađimo gradijent skalarnog polja iz primjera
4.4.
Rješenje.
Ako vektor
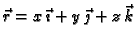
napišemo u obliku
onda dobivamo
gdje je
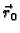
jedinični vektor u smjeru vektora
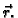
Primijetimo da je
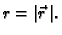
Primjer 4.10
Naći
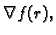
gdje je
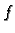
derivabilna funkcija, dok je
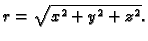
Rješenje. U primjeru 4.9 vidimo da je
Prema tome
Neka je dano skalarno polje 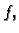 točka
točka
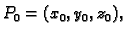 i
jedinični vektor
i
jedinični vektor
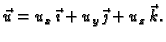 Neka je točka
Neka je točka
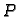 udaljena od
udaljena od 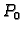 za
za 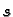 u smjeru vektora
u smjeru vektora 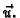
Figure 4.4:
Derivacija skalarnog polja u smjeru.
|
|
Iz slike vidimo da je
Tako za zadanu točku 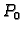 i zadani smjer
i zadani smjer
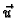 imamo složenu funkciju od jedne varijable
Očito je
imamo složenu funkciju od jedne varijable
Očito je
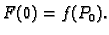 Interesira nas što se događa s kvocijentom
kad
Interesira nas što se događa s kvocijentom
kad 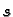 teži k nuli preko pozitivnih vrijednosti. S tim u vezi imamo
sljedeću definiciju.
teži k nuli preko pozitivnih vrijednosti. S tim u vezi imamo
sljedeću definiciju.
Definicija 38
Neka je
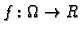
skalarno polje. Neka je
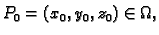
neka je dan jedinični vektor
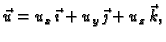
i neka
je
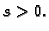
Broj
ako postoji, zove se
derivacija skalarnog polja 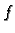 u smjeru vektora
u smjeru vektora 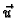 u
točki
u
točki 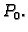
Derivacija u smjeru je
dakle
Skalarni
produkt vektora s jediničnim vektorom 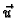 je skalarna
komponenta projekcije vektora na pravac kroz
je skalarna
komponenta projekcije vektora na pravac kroz 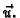
Figure 4.5:
Derivacija u smjeru.
|
|
Prema tome
derivacija u smjeru će biti najveća, ako vektor 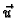 izaberemo
u smjeru
izaberemo
u smjeru 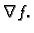 S druge strane, po definiciji derivacija u smjeru
će biti najveća, ako izaberemo smjer najbržeg rasta skalarnog polja
S druge strane, po definiciji derivacija u smjeru
će biti najveća, ako izaberemo smjer najbržeg rasta skalarnog polja
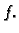 Dakle, možemo zaključiti da gradijent skalarnog polja
pokazuje smjer njegovog najbržeg rasta.
Dakle, možemo zaključiti da gradijent skalarnog polja
pokazuje smjer njegovog najbržeg rasta.
Neka je 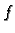 skalarno polje klase
skalarno polje klase 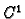 na nekom području u
prostoru. Ako stavimo
na nekom području u
prostoru. Ako stavimo
onda skup točaka koje
zadovoljavaju tu jednadžbu predstavlja plohu 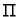 u prostoru. Ploha
u prostoru. Ploha
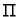 je nivoploha polja
je nivoploha polja 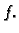 Neka je
Neka je
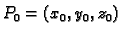 proizvoljna
točka u
proizvoljna
točka u 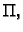 neka tom točkom prolazi glatka krivulja
neka tom točkom prolazi glatka krivulja 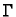 (Jordanov luk)
koja potpuno leži u plohi
(Jordanov luk)
koja potpuno leži u plohi 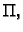 i neka je
i neka je
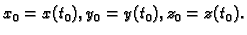 Tada, za svaki
Tada, za svaki 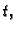 vrijedi
Ako ovu jednakost deriviramo po
vrijedi
Ako ovu jednakost deriviramo po 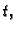 dobivamo
gdje je
dobivamo
gdje je
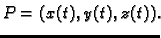 Specijalno za
Specijalno za 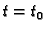 imamo
Kako je
imamo
Kako je
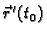 vektor tangente na krivulju
vektor tangente na krivulju 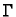 u
točki
u
točki 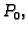 i prema tome leži u tangencijalnoj ravnini u točki
i prema tome leži u tangencijalnoj ravnini u točki
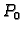 na plohu
na plohu 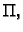 i kako je krivulja
i kako je krivulja 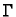 proizvoljna, slijedi
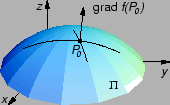
da je gradijent skalarnog polja u točki
proizvoljna, slijedi
da je gradijent skalarnog polja u točki 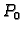 okomit na nivoplohu
kroz tu točku. Budući da je točka
okomit na nivoplohu
kroz tu točku. Budući da je točka 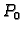 proizvoljna točka
nivoplohe, slijedi da je gradijent okomit na nivoplohu u proizvoljnoj
točki te plohe.
proizvoljna točka
nivoplohe, slijedi da je gradijent okomit na nivoplohu u proizvoljnoj
točki te plohe.
Možemo zaključiti da skalarno polje najbrže raste u smjeru okomitom
na nivoplohu.
Definicija 39
Neka je
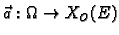
vektorsko polje. Neka je
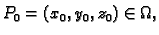
neka je dan jedinični vektor
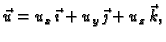
i neka
je
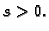
Vektor
ako postoji,
zove se
derivacija vektorskog polja 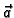 u smjeru vektora
u smjeru vektora
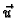 u točki
u točki 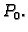
Figure 4.6:
Derivacija vektorskog polja u smjeru.
|
|
Neka je
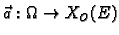 vektorsko polje klase
vektorsko polje klase
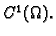 Neka je
Neka je
Stavimo
Tada je
Svaka od skalarnih komponenti je
derivacija odgovarajućeg skalarnog polja u smjeru, pa imamo
- 1.
- Definirajte skalarno polje. Dajte primjere.
- 2.
- Definirajte vektorsko polje. Dajte primjere.
- 3.
- Definirajte gradijent skalarnog polja. Koja su njegova svojstva?
- 4.
- Kako se definira derivacija skalarnog polja u smjeru? Kako se
računa?
- 5.
- Što se može reći o smjeru određenom gradijentom skalarnog
polja u vezi s tim poljem?
- 6.
- Definirajte derivaciju vektorskog polja u smjeru. Kojom formulom
se računa?
- 1.
- Izvesti formulu za vektorsko polje iz primjera 4.8.
Rješenje. Pretpostavimo da je koordinatni sustav postavljen tako da je os
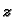 os cilindra, da je jedna baza u ravnini
os cilindra, da je jedna baza u ravnini 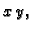 a druga u
ravnini
a druga u
ravnini 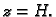 Nađimo polje pomaka. Po pretpostavci kut zakreta
Nađimo polje pomaka. Po pretpostavci kut zakreta
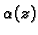 se povećava proporcionalno visini
se povećava proporcionalno visini
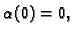 i
i
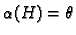 daje
Dakle, u poprečnom presjeku na visini
daje
Dakle, u poprečnom presjeku na visini 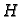 radi se o rotaciji u
ravnini okomitoj na os
radi se o rotaciji u
ravnini okomitoj na os 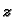 za kut
za kut
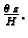 Ako je
materijalna točka na početku imala koordinate
nakon torzije imat će koordinate
Ako je
materijalna točka na početku imala koordinate
nakon torzije imat će koordinate
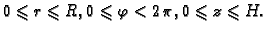 Vektorsko polje
pomaka je tako
Nakon primjene adicionih formula dobivamo
Odatle
Primijetimo da za vrlo male torzije, tj. za
Vektorsko polje
pomaka je tako
Nakon primjene adicionih formula dobivamo
Odatle
Primijetimo da za vrlo male torzije, tj. za
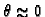 imamo
imamo
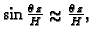 i
i
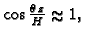 pa je u tom slučaju vektorsko
polje pomaka
pa je u tom slučaju vektorsko
polje pomaka
- 2.
- Naći
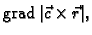 gdje je
gdje je
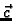 konstantno vektorsko polje, a
konstantno vektorsko polje, a
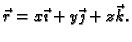
Rješenje.
pa je
Zbog svojstava mješovitog i vektorsko-vektorskog produkta vektora, imamo
Iz primjera 4.10 slijedi
Zatim
Dakle
- 3.
- Naći derivaciju skalarnog polja
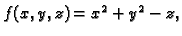 u točki
u točki
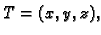 u smjeru radijvektora točke
u smjeru radijvektora točke 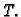
Rješenje. Jedinični vektor u smjeru radijvektora točke 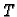 je
je
Zatim
Dakle
- 4.
- Naći derivaciju gradijenta skalarnog polja
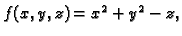 u točki
u točki
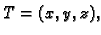 u smjeru radijvektora
točke
u smjeru radijvektora
točke 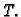
Rješenje. Iz prethodnog zadatka
Odatle




Next: Divergencija i rotacija. Specijalna
Up: Polja
Previous: Polja
Contents
Index
Salih Suljagic
2000-03-11
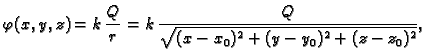
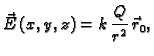
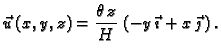
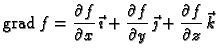
![]() možemo shvatiti kao djelovanje diferencijalnog
operatora
možemo shvatiti kao djelovanje diferencijalnog
operatora
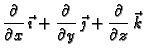
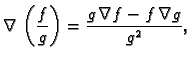
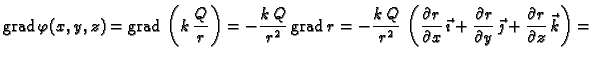
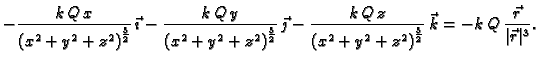
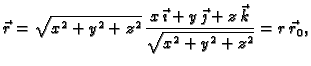
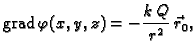
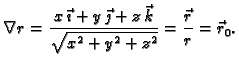
![]() točka
točka
![]() i
jedinični vektor
i
jedinični vektor
![]() Neka je točka
Neka je točka
![]() udaljena od
udaljena od ![]() za
za ![]() u smjeru vektora
u smjeru vektora ![]()
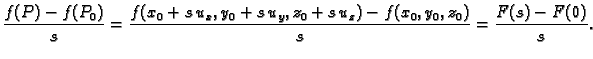
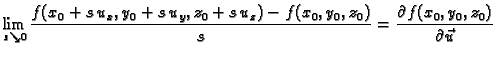
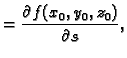
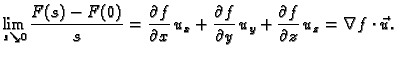
![]() skalarno polje klase
skalarno polje klase ![]() na nekom području u
prostoru. Ako stavimo
na nekom području u
prostoru. Ako stavimo
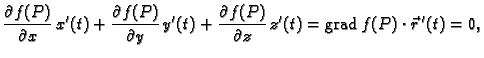
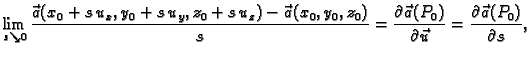
![]() vektorsko polje klase
vektorsko polje klase
![]() Neka je
Neka je
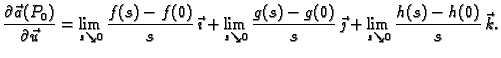
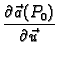
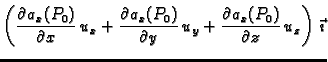
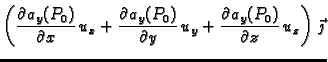
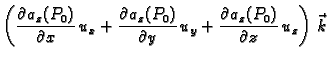
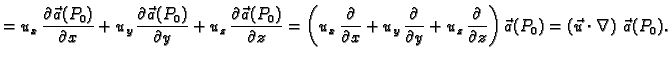
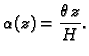
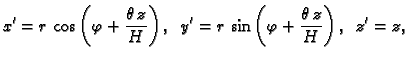
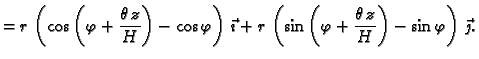
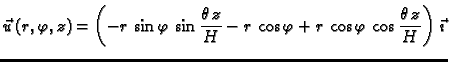
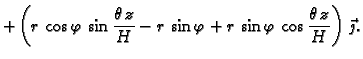
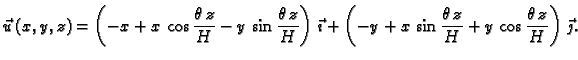
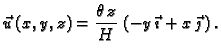
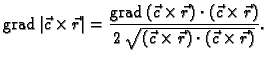
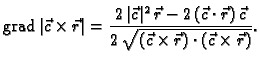
![]() je
je