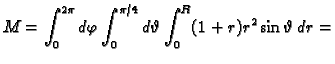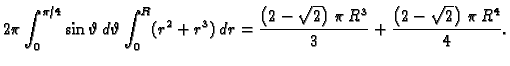



Next: Primjene integrala
Up: Višestruki integrali
Previous: Trostruki integral
Contents
Index
Subsections
Polarni koordinatni sustav u ravnini
Neka je u ravnini dana točka 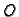 i zraka (polupravac) kojoj je vrh
točka
i zraka (polupravac) kojoj je vrh
točka 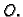 Odredimo na polupravcu točku
Odredimo na polupravcu točku 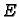 koja je različita od
koja je različita od
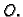 Na poznati način (kao na brojevnom pravcu) možemo na polupravac
nanijeti nenegativne realne brojeve. Svakoj točki
Na poznati način (kao na brojevnom pravcu) možemo na polupravac
nanijeti nenegativne realne brojeve. Svakoj točki 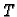 u ravnini
možemo pridružiti broj
u ravnini
možemo pridružiti broj 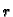 udaljenost točke
udaljenost točke 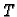 od
od 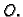 Ako je
Ako je
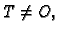 onda točki
onda točki 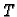 možemo također pridružiti kut
možemo također pridružiti kut 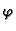 što ga dužina
što ga dužina
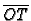 zatvara s polupravcem.
zatvara s polupravcem.
Figure 2.10:
Polarni koordinatni sustav u ravnini.
|
|
Taj kut
smatramo pozitivnim, ako se od polupravca do dužine
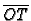 ide kruženjem protivnim kruženju kazaljke na satu. U drugom slučaju
kut smatramo negativnim. Za
ide kruženjem protivnim kruženju kazaljke na satu. U drugom slučaju
kut smatramo negativnim. Za 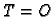 kut
kut 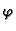 nije određen. Točka
nije određen. Točka
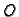 je jednoznačno određena time da je
je jednoznačno određena time da je 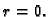 Tako točki
Tako točki 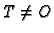 možemo pridružiti uređeni par brojeva
možemo pridružiti uređeni par brojeva
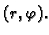 Pri tom je
Pri tom je
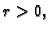 a
a
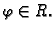 Ako je
onda je
Dakle, jednoj točki
Ako je
onda je
Dakle, jednoj točki 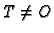 je pridruženo beskonačno mnogo uređenih
parova
je pridruženo beskonačno mnogo uređenih
parova
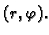
Obratno, svakom uređenom paru realnih brojeva
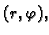 tako da je
tako da je
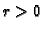 i
i
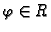 je pridružena jedna točka
je pridružena jedna točka 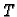 u ravnini
različita od
u ravnini
različita od 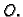
Ovo pridruživanje se zove polarni koordinatni
sustav u ravnini. Imamo
sljedeće oznake. Točka 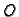 se zove pol,
polupravac se zove polarna os, brojevi
se zove pol,
polupravac se zove polarna os, brojevi 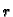 i
i 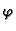 se zovu
polarne koordinate.
se zovu
polarne koordinate.
Ako u ravnini zadamo Kartezijev pravokutni koordinatni sustav i polarni
sustav tako da se ishodište poklopi s polom, a polarna os s nenegativnim
polupravcem osi 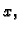 onda je veza između jednih i drugih koordinata dana
formulama
onda je veza između jednih i drugih koordinata dana
formulama
odnosno
Primjer 2.7
Neka je dana točka
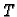
s Kartezijevim koordinatama
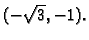
Naći polarne koordinate.
Rješenje.
Odatle slijedi
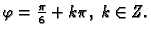
Budući da se točka
nalazi u trećem kvadrantu,
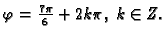
Primjer 2.8
U polarnom koordinatnom sustavu naći jednadžbu krivulje,
koja u Kartezijevom sustavu ima jednadžbu
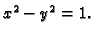
Rješenje
Cilindrični koordinatni sustav
Točka u prostoru je u cilindričnom sustavu dana s tri koordinate
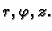 Pri tom je
Pri tom je 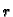 udaljenost projekcije
udaljenost projekcije 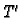 točke
točke 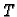 na
ravninu
na
ravninu 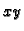 od ishodišta,
od ishodišta, 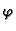 je kut što ga dužina
je kut što ga dužina
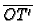 zatvara s osi
zatvara s osi 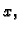
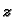 ima isto značenje kao u
Kartezijevom koordinatnom sustavu.
ima isto značenje kao u
Kartezijevom koordinatnom sustavu.
Figure 2.11:
Cilindrični koordinatni sustav u prostoru.
|
|
Iz ovoga proizlaze formule
Osim toga vrijedi
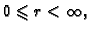
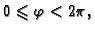
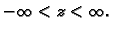 Koordinatne plohe se dobiju kad se neka koordinata
pretpostavi konstantnom. Tako za
Koordinatne plohe se dobiju kad se neka koordinata
pretpostavi konstantnom. Tako za 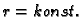 imamo kružni cilindar,
čija je os os
imamo kružni cilindar,
čija je os os 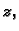 osim u slučaju
osim u slučaju 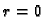 kad se radi o osi
kad se radi o osi 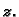 Ploha
Ploha
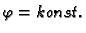 je poluravnina okomita na ravninu
je poluravnina okomita na ravninu 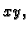 čiji je rub
os
čiji je rub
os 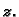 Ploha
Ploha 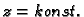 je ravnina paralelna s ravninom
je ravnina paralelna s ravninom 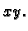
Primjer 2.9
Točka
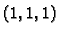
u kartezijevom koordinatnom sustavu ima
u cilindričnom sustavu koordinate
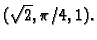
Primjer 2.10
Jednokrilni kružni hiperboloid
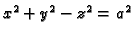
ima u cilindričnom
sustavu jednadžbu
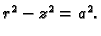
Sferni koordinatni sustav
Točka u prostoru je u sfernom sustavu dana s tri koordinate
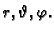 Pri tom je
Pri tom je 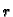 udaljenost točke
udaljenost točke 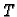 od ishodišta,
od ishodišta,
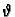 je kut što ga dužina
je kut što ga dužina
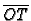 zatvara s osi
zatvara s osi 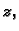
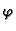 je kut što ga projekcija
je kut što ga projekcija
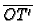 dužine
dužine
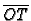 na ravninu
na ravninu 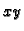 zatvara s osi
zatvara s osi 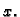
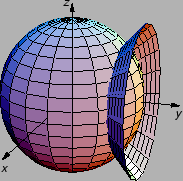
Figure 2.12:
Sferni koordinatni sustav u prostoru.
|
|
Iz ovoga proizlaze
formule
Osim toga vrijedi
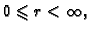
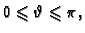
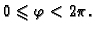 Ploha
Ploha 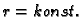 je sfera sa središtem u
ishodištu i radiusom
je sfera sa središtem u
ishodištu i radiusom 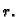 Ploha
Ploha
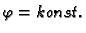 je poluravnina
okomita na ravninu
je poluravnina
okomita na ravninu 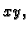 čiji je rub os
čiji je rub os 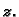 Ploha
Ploha
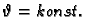 je
stožasta ploha čija je os os
je
stožasta ploha čija je os os 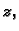 a kut izvodnice prema pozitivnom
dijelu osi
a kut izvodnice prema pozitivnom
dijelu osi 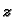 je
je
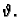
Primjer 2.11
Točka
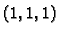
u kartezijevom koordinatnom sustavu ima
u sfernom sustavu koordinate
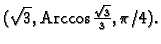
Primjer 2.12
Jednokrilni kružni hiperboloid
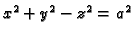
ima u
sfernom
sustavu jednadžbu
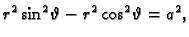
tj.
Oblik podintegralne funkcije ili oblik područja integracije nam neki
puta sugeriraju prelazak iz Kartezijevog u neki drugi
koordinatni sustav. Za definiciju dvostrukog i trostrukog integrala
bile su važne površine pravokutnika 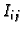 i kvadra
i kvadra 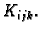 Pravokutnik
Pravokutnik 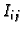 je lik, koji se nalazi između koordinatnih
linija
je lik, koji se nalazi između koordinatnih
linija
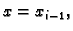
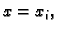
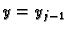 i
i 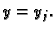 Tome u polarnom
koordinatnom sustavu u ravnini odgovara lik omeđen koordinatnim
linijama
Tome u polarnom
koordinatnom sustavu u ravnini odgovara lik omeđen koordinatnim
linijama
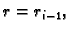
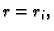
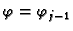 i
i
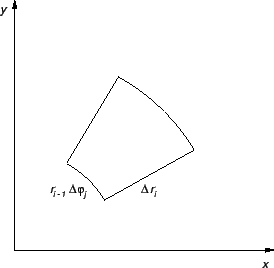
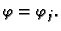 To je lik kao na slici, s tim da smo upotrebili
oznake
To je lik kao na slici, s tim da smo upotrebili
oznake
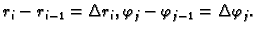
Površina tog lika je približno
Tako, ako želimo dvostruki integral
računati prelaskom u polarni sustav u ravnini, onda koristimo formulu
Ovdje je 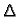 isto područje, no kako se nalazimo u drugom
koordinatnom sustavu, njegove su granice drugačije.
isto područje, no kako se nalazimo u drugom
koordinatnom sustavu, njegove su granice drugačije.
Primjer 2.13
Izračunati
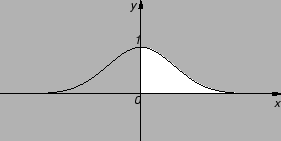
Rješenje. Prema jednom prethodnom primjeru
Prelaskom na polarni sustav u ravnini imamo
Tako je
Kod definicije trostrukog integrala podjelu smo vršili na
manje kvadre. Kvadar 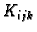 je omeđen koordinatnim plohama
je omeđen koordinatnim plohama
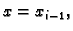
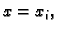
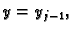
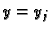 i
i
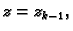
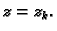 Takvom kvadru u cilindričnom koordinatnom sustavu u prostoru odgovara tijelo
omeđeno koordinatnim plohama
Takvom kvadru u cilindričnom koordinatnom sustavu u prostoru odgovara tijelo
omeđeno koordinatnim plohama
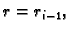
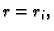
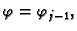
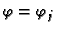 i
i
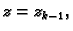
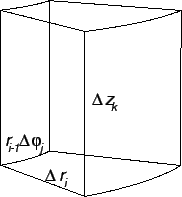
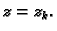 To je tijelo prikazano na slici, gdje smo koristili sljedeće oznake
To je tijelo prikazano na slici, gdje smo koristili sljedeće oznake
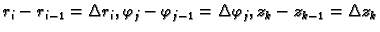
Volumen tog tijela je približno
Tako, ako želimo trostruki
integral računati prelaskom u cilindrični sustav u prostoru, onda
koristimo formulu
Ovdje je 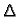 isto područje, no kako se nalazimo u drugom koordinatnom
sustavu, njegove su granice drugačije.
isto područje, no kako se nalazimo u drugom koordinatnom
sustavu, njegove su granice drugačije.
Primjer 2.14
Naći volumen tijela omeđenog plohama
Rješenje. Prelaskom u cilindrični koordinatni sustav imamo
Kvadru 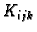 u sfernom koordinatnom sustavu u prostoru
odgovara tijelo omeđeno koordinatnim plohama
u sfernom koordinatnom sustavu u prostoru
odgovara tijelo omeđeno koordinatnim plohama
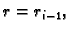
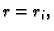
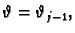
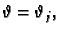
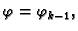 i
i
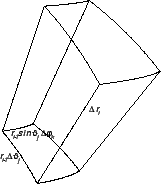
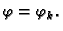 To tijelo je dano na slici, gdje smo uveli oznake
To tijelo je dano na slici, gdje smo uveli oznake
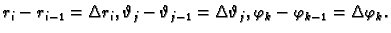
Volumen tog tijela je približno
Tako, ako želimo trostruki integral računati prelaskom u sferni koordinatni
sustav u prostoru, onda koristimo formulu
Ovdje je 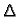 isto područje, no kako se nalazimo u drugom koordinatnom
sustavu, njegove su granice drugačije.
isto područje, no kako se nalazimo u drugom koordinatnom
sustavu, njegove su granice drugačije.
Primjer 2.15
Volumen kugle radiusa
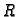
je
U gornjim razmatranjima smo za računanje integrala u novom koordinatnom
sustavu trebali naći formulu za površinu odnosno volumen u novom
koordinatnom sustavu. Ako je dana općenita transformacija u novi
koordinatni sustav u ravnini, na pr.
onda se faktor, kojim pod integralom treba množiti 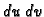 računa kao
apsolutna vrijednost determinante
računa kao
apsolutna vrijednost determinante
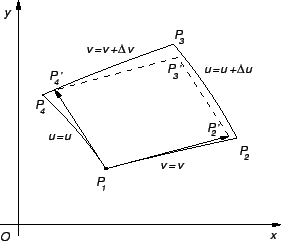
Da bismo objasnili zašto se pojavljuje taj faktor, uočimo lik koji
je omeđen koordinatnim linijama
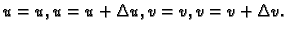
Njegovi vrhovi su točke
Površinu ovog lika ćemo izračunati
približno, tako da izračunamo površinu paralelograma čiji su
vrhovi
Taj paralelogram je
razapet vektorima
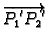 i
i
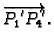 čije su komponente
Njegova je površina jednaka duljini
vektorskog produkta tih vektora, a to je apsolutna
vrijednost sljedeće determinante
čije su komponente
Njegova je površina jednaka duljini
vektorskog produkta tih vektora, a to je apsolutna
vrijednost sljedeće determinante
Primjer 2.16
Naći površinu lika koji omeđuje elipsa
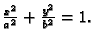
Rješenje. Uvedimo novi koordinatni sustav u ravnini
Ako je dana općenita transformacija u novi koordinatni sustav u
prostoru, na pr.
onda se faktor, kojim pod integralom treba množiti
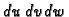 računa kao apsolutna vrijednost determinante
Determinanta
računa kao apsolutna vrijednost determinante
Determinanta 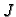 se zove Jacobijan.
se zove Jacobijan.
Objašnjenje je slično onome kod istog problema za dvije
varijable. Sada su ključne točke
Vektori
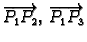 i
i
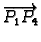 imaju komponente
Apsolutna vrijednost mješovitog produkta tih vektora daje upravo
volumen paralelepipeda koji je s njima razapet, a to je približno
ono što tražimo.
imaju komponente
Apsolutna vrijednost mješovitog produkta tih vektora daje upravo
volumen paralelepipeda koji je s njima razapet, a to je približno
ono što tražimo.
Primjer 2.17
Naći volumen tijela omeđenog elipsoidom
Rješenje. Stavimo
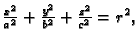
pa je elipsoid u
zadatku koordinatna ploha
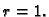
Jacobijan je
Dakle
- 1.
- Opišite cilindrični i sferni koordinatni sustav u prostoru.
- 2.
- Kako izgleda formula za integriranje u polarnom koordinatnom
sustavu u ravnini? Objasnite.
- 3.
- Kako izgleda formula za integriranje u cilindričnom
koordinatnom sustavu u prostoru? Objasnite.
- 4.
- Kako izgleda formula za integriranje u sfernom
koordinatnom sustavu u prostoru? Objasnite.
- 5.
- Objasnite što je Jacobijan, kako se računa i koja je njegova
uloga prilikom integriranja.
- 1.
- Naći površinu lika što ga omeđuje asteroida
Figure 2.13:
Lik omeđen asteroidom.
|
|
Uvedimo novi koordinatni sustav u ravninu
Područje koje omeđuje asteroida je u tim koordinatama dano s
- 2.
- Naći masu tijela omeđenog plohama
ako je gustoća mase
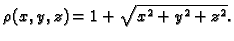
Rješenje. Taj zadatak je ekvivalentan zadatku u kojem je
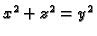 zamijenjeno s
zamijenjeno s
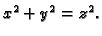 Na slici se ta zamjena realizira tako da
osi
Na slici se ta zamjena realizira tako da
osi 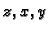 postaju redom osi
postaju redom osi 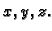 U tom slučaju granice
integracije su jednostavnije.
U tom slučaju granice
integracije su jednostavnije.




Next: Primjene integrala
Up: Višestruki integrali
Previous: Trostruki integral
Contents
Index
Salih Suljagic
2000-03-11
![]() i zraka (polupravac) kojoj je vrh
točka
i zraka (polupravac) kojoj je vrh
točka ![]() Odredimo na polupravcu točku
Odredimo na polupravcu točku ![]() koja je različita od
koja je različita od
![]() Na poznati način (kao na brojevnom pravcu) možemo na polupravac
nanijeti nenegativne realne brojeve. Svakoj točki
Na poznati način (kao na brojevnom pravcu) možemo na polupravac
nanijeti nenegativne realne brojeve. Svakoj točki ![]() u ravnini
možemo pridružiti broj
u ravnini
možemo pridružiti broj ![]() udaljenost točke
udaljenost točke ![]() od
od ![]() Ako je
Ako je
![]() onda točki
onda točki ![]() možemo također pridružiti kut
možemo također pridružiti kut ![]() što ga dužina
što ga dužina
![]() zatvara s polupravcem.
zatvara s polupravcem.
![]() tako da je
tako da je
![]() i
i
![]() je pridružena jedna točka
je pridružena jedna točka ![]() u ravnini
različita od
u ravnini
različita od ![]()
![]() se zove pol,
polupravac se zove polarna os, brojevi
se zove pol,
polupravac se zove polarna os, brojevi ![]() i
i ![]() se zovu
polarne koordinate.
se zovu
polarne koordinate.
![]() onda je veza između jednih i drugih koordinata dana
formulama
onda je veza između jednih i drugih koordinata dana
formulama
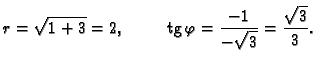
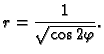
![]() Pri tom je
Pri tom je ![]() udaljenost projekcije
udaljenost projekcije ![]() točke
točke ![]() na
ravninu
na
ravninu ![]() od ishodišta,
od ishodišta, ![]() je kut što ga dužina
je kut što ga dužina
![]() zatvara s osi
zatvara s osi ![]()
![]() ima isto značenje kao u
Kartezijevom koordinatnom sustavu.
ima isto značenje kao u
Kartezijevom koordinatnom sustavu.
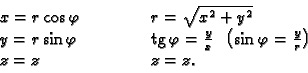

![]() Pri tom je
Pri tom je ![]() udaljenost točke
udaljenost točke ![]() od ishodišta,
od ishodišta,
![]() je kut što ga dužina
je kut što ga dužina
![]() zatvara s osi
zatvara s osi ![]()
![]() je kut što ga projekcija
je kut što ga projekcija
![]() dužine
dužine
![]() na ravninu
na ravninu ![]() zatvara s osi
zatvara s osi ![]()
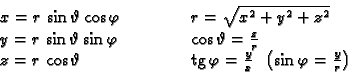

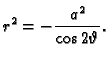
![]() i kvadra
i kvadra ![]() Pravokutnik
Pravokutnik ![]() je lik, koji se nalazi između koordinatnih
linija
je lik, koji se nalazi između koordinatnih
linija
![]()
![]()
![]() i
i ![]() Tome u polarnom
koordinatnom sustavu u ravnini odgovara lik omeđen koordinatnim
linijama
Tome u polarnom
koordinatnom sustavu u ravnini odgovara lik omeđen koordinatnim
linijama
![]()
![]()
![]() i
i
![]() To je lik kao na slici, s tim da smo upotrebili
oznake
To je lik kao na slici, s tim da smo upotrebili
oznake
![]()
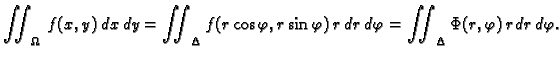
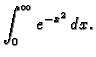
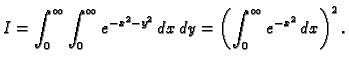
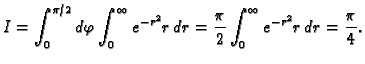
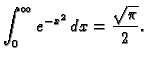
![]() je omeđen koordinatnim plohama
je omeđen koordinatnim plohama
![]()
![]()
![]()
![]() i
i
![]()
![]() Takvom kvadru u cilindričnom koordinatnom sustavu u prostoru odgovara tijelo
omeđeno koordinatnim plohama
Takvom kvadru u cilindričnom koordinatnom sustavu u prostoru odgovara tijelo
omeđeno koordinatnim plohama
![]()
![]()
![]()
![]() i
i
![]()
![]() To je tijelo prikazano na slici, gdje smo koristili sljedeće oznake
To je tijelo prikazano na slici, gdje smo koristili sljedeće oznake
![]()
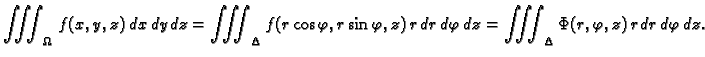
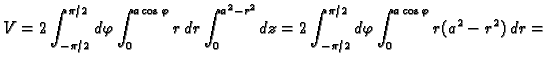
![]() u sfernom koordinatnom sustavu u prostoru
odgovara tijelo omeđeno koordinatnim plohama
u sfernom koordinatnom sustavu u prostoru
odgovara tijelo omeđeno koordinatnim plohama
![]()
![]()
![]()
![]()
![]() i
i
![]() To tijelo je dano na slici, gdje smo uveli oznake
To tijelo je dano na slici, gdje smo uveli oznake
![]()
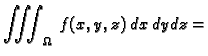
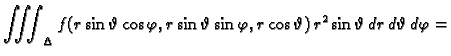
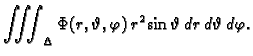
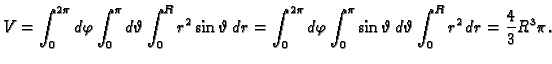
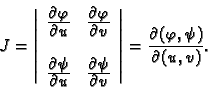
![]()
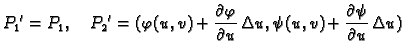
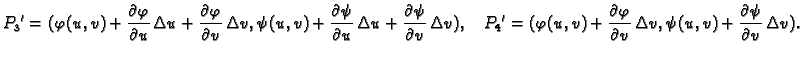
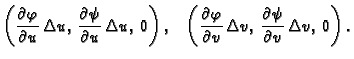
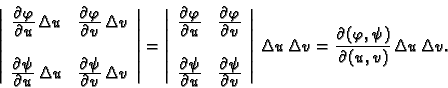
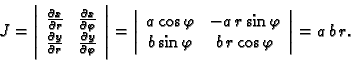
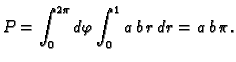
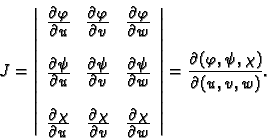
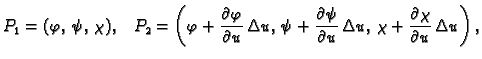
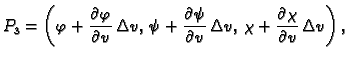
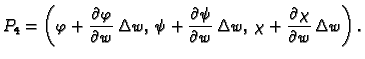
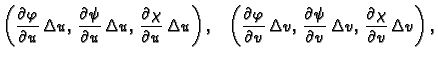
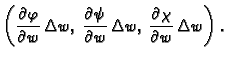
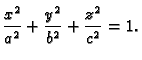
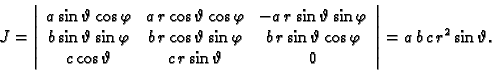
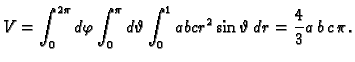
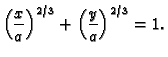
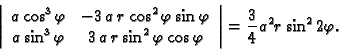
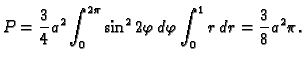
![]() zamijenjeno s
zamijenjeno s
![]() Na slici se ta zamjena realizira tako da
osi
Na slici se ta zamjena realizira tako da
osi ![]() postaju redom osi
postaju redom osi ![]() U tom slučaju granice
integracije su jednostavnije.
U tom slučaju granice
integracije su jednostavnije.