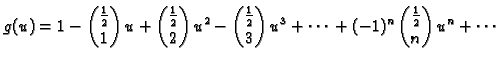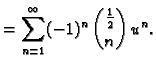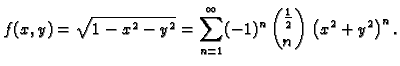



Next: Ekstremi funkcija više varijabli
Up: Diferencijalni račun
Previous: Teorem srednje vrijednosti
Contents
Index
Subsections
Neka je 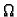 područje u
područje u 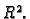 Prva derivacija funkcije
Prva derivacija funkcije
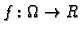 u točki
u točki
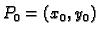 je polinom
je polinom
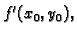 prvog stupnja od dvije varijable
prvog stupnja od dvije varijable 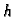 i
i 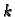 zadan
formulom
zadan
formulom
Druga derivacija funkcije 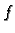 u točki
u točki
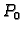 (drugi diferencijal) je polinom
(drugi diferencijal) je polinom
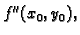 drugog stupnja od dvije varijable
drugog stupnja od dvije varijable 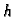 i
i 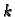 zadan formulom
treća
derivacija (treći diferencijal) funkcije
zadan formulom
treća
derivacija (treći diferencijal) funkcije
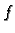 u točki
u točki 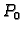 je polinom
je polinom
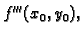 trećeg stupnja od
dvije varijable
trećeg stupnja od
dvije varijable 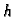 i
i 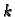 zadan formulom
i t.d.
zadan formulom
i t.d.
Općenito, 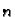 -ta derivacija (
-ta derivacija (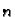 -ti
diferencijal) funkcije
-ti
diferencijal) funkcije 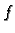 u točki
u točki 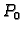 je polinom
je polinom 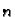 -tog stupnja
od dvije varijable
-tog stupnja
od dvije varijable 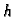 i
i 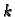 zadan formulom
zadan formulom
Koristeći formulu binomnog teorema možemo derivaciju 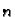 -tog reda
kraće zapisati formalno ovako
-tog reda
kraće zapisati formalno ovako
Zapis je
doista formalan, jer se eksponent 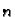 pojavljuje kao eksponent kad se
radi o
pojavljuje kao eksponent kad se
radi o 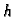 i
i 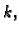 a predstavlja red derivacije kad se odnosi na
a predstavlja red derivacije kad se odnosi na
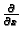 i
i
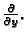
Pri tom treba naglasiti da je 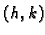 pomak od točke
pomak od točke 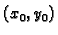 do
točke
do
točke
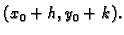 Ako stavimo
Ako stavimo 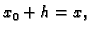
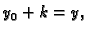 onda je
onda je
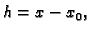
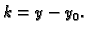
Primjer 1.34
Naći
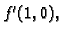
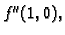
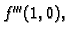
ako je
Rješenje. Potrebne derivacije su
pa je
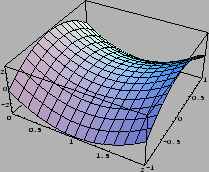
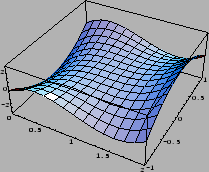
Na sljedećim slikama se vide plohe, koje su grafovi ovih funkcija.
Teorem 12
(Taylorov, srednje vrijednosti) Neka je
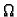
područje u
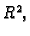
i neka je
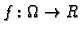
funkcija klase
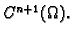
Neka su
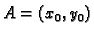
i
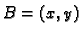
točke u
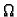
takve, da spojnica
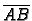
leži u
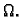
Tada postoji točka
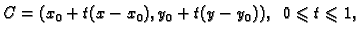
na
spojnici
takva, da je
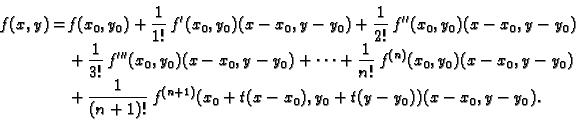 |
(1.4) |
Dokaz.
Formula (1.4) se zove Taylorova formula.
Njezina desna
strana se sastoji od dva dijela. Polinom
se zove Taylorov
polinom 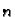 -tog stupnja, a
se zove
-tog stupnja, a
se zove
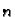 -ti ostatak.
-ti ostatak.
Dakle, Taylorovu formulu možemo shvatiti kao aproksimaciju funkcije
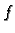 u točki
u točki
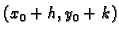 pomoću polinoma od dvije varijable
pomoću polinoma od dvije varijable 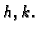 Greška te aproksimacije je
Greška te aproksimacije je 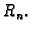
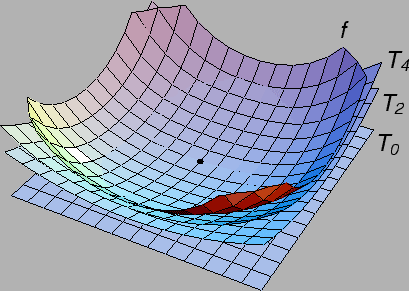
Na sljedećoj slici se vidi
kako Taylorovi polinomi sve bolje aproksimiraju funkciju
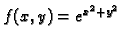 u okolini točke
u okolini točke 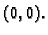 Polinomi
Polinomi 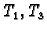 nisu
ucrtani, jer je
nisu
ucrtani, jer je 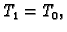 i
i 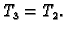
Taylorov polinom ima važno svojstvo da se njegova vrijednost i
vrijednosti njegovih derivacija poklapaju s vrijednostima funkcije i
odgovarajućih derivacija u točki
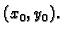 Radi jednostavnosti
pokažimo da to vrijedi za Taylorov polinom drugog stupnja.
Radi jednostavnosti
pokažimo da to vrijedi za Taylorov polinom drugog stupnja.
Odatle
Da ustanovimo jednakost prvih derivacija od 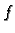 i
i 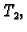 u točki
u točki
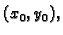 dovoljno je ustanoviti da su prve parcijalne derivacije
tih funkcija u točki
dovoljno je ustanoviti da su prve parcijalne derivacije
tih funkcija u točki 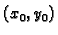 jednake.
i prema tome
Slično
i prema tome
Dakle
Za jednakost drugih derivacija od
jednake.
i prema tome
Slično
i prema tome
Dakle
Za jednakost drugih derivacija od 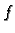 i
i 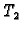 u točki
u točki
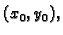 dovoljno je ustanoviti jednakost drugih parcijalnih derivacija. Imamo
i prema tome
dovoljno je ustanoviti jednakost drugih parcijalnih derivacija. Imamo
i prema tome
Primjer 1.35
Naći Taylorovu formulu funkcije
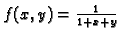
u
točki
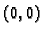
za
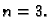
Rješenje.
Tako imamo
Neka je 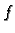 klase
klase
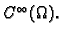 U tom slučaju imamo Taylorovu
formulu za bilo koji
U tom slučaju imamo Taylorovu
formulu za bilo koji 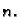 Ako je pri tom još
Ako je pri tom još
za neki  onda Taylorova formula (1.4) prelazi u formulu
onda Taylorova formula (1.4) prelazi u formulu
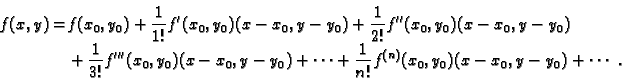 |
(1.5) |
Red na desnoj strani formule 1.5 se zove Taylorov
red. Ako je
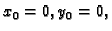 onda imamo McLaurinov red
Formula (1.5) izražava dvije činjenice: da red na
desnoj strani konvergira u točki
onda imamo McLaurinov red
Formula (1.5) izražava dvije činjenice: da red na
desnoj strani konvergira u točki 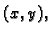 i da je njegova suma
jednaka vrijednosti funkcije u točki
i da je njegova suma
jednaka vrijednosti funkcije u točki 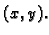 Skup onih
Skup onih 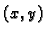 za
koje Taylorov red konvergira, općenito nije jednak domeni funkcije.
To se dobro vidi na sljedećem primjeru.
za
koje Taylorov red konvergira, općenito nije jednak domeni funkcije.
To se dobro vidi na sljedećem primjeru.
Primjer 1.36
Naći Taylorov red funkcije
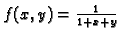
u
točki
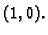
Rješenje. Domena funkcije je
Dakle
Figure 1.13:
a) Domena funkcije. b) Područje konvergencije Taylorovog reda funkcije.
|
|
Umjesto da se računa
-ta derivacija, što je često mukotrpno,
možemo koristiti geometrijski red
Pri tom ova jednakost vrijedi samo za
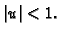
U našem slučaju
Pri tom red konvergira i to k vrijednosti funkcije za one
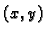
za koje je
tj.
što se svodi na
odnosno na slici
Primjer 1.37
Naći McLaurinov red funkcije
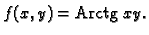
Rješenje. Također možemo izbjeći deriviranje na sljedeći način
Stavimo
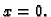
Dobivamo
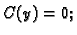
dakle
- 1.
- Definirajte derivacije višeg reda funkcije u točki.
- 2.
- Kako se one formalno mogu kraće zapisati?
- 3.
- Kako glasi Taylorov teorem srednje vrijednosti?
- 4.
- Napišite Taylorov polinom
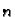 -tog reda funkcije
-tog reda funkcije 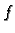 u točki
u točki
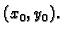
- 5.
- U kom smislu Taylorov polinom aproksimira funkciju?
- 6.
- Koje važno svojstvo ima Taylorov polinom?
- 7.
- Što je Taylorov, a što McLaurinov red funkcije
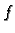 ?
?
- 8.
- Što se može reći o jednakosti funkcije i njezinog Taylorovog reda?
- 1.
- Naći prvu derivaciju funkcije
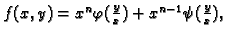 pod pretpostavkom da su
funkcije
pod pretpostavkom da su
funkcije 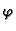 i
i 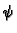 neprekidno derivabilne.
neprekidno derivabilne.
Rješenje. Prve parcijalne derivacije su
pa je
- 2.
- Naći Taylorov polinom trećeg stupnja funkcije
u okolini točke
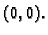
Rješenje. Potrebne derivacije su
Tako je
Prema tome, Taylorov polinom je
- 3.
- Naći McLaurinov red funkcije
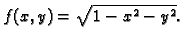
Rješenje. Uvedemo li novu varijablu
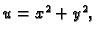 imamo
imamo
Prema razvoju u binomni red slijedi
Odatle




Next: Ekstremi funkcija više varijabli
Up: Diferencijalni račun
Previous: Teorem srednje vrijednosti
Contents
Index
Salih Suljagic
2000-03-11
![]() područje u
područje u ![]() Prva derivacija funkcije
Prva derivacija funkcije
![]() u točki
u točki
![]() je polinom
je polinom
![]() prvog stupnja od dvije varijable
prvog stupnja od dvije varijable ![]() i
i ![]() zadan
formulom
zadan
formulom
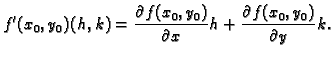
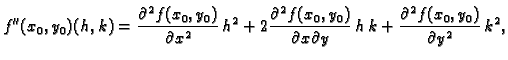
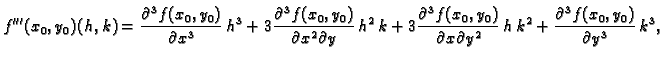
![]() -ta derivacija (
-ta derivacija (![]() -ti
diferencijal) funkcije
-ti
diferencijal) funkcije ![]() u točki
u točki ![]() je polinom
je polinom ![]() -tog stupnja
od dvije varijable
-tog stupnja
od dvije varijable ![]() i
i ![]() zadan formulom
zadan formulom
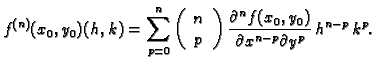
![]() -tog reda
kraće zapisati formalno ovako
-tog reda
kraće zapisati formalno ovako
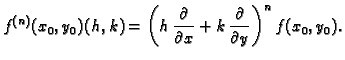
![]() pomak od točke
pomak od točke ![]() do
točke
do
točke
![]() Ako stavimo
Ako stavimo ![]()
![]() onda je
onda je
![]()
![]()
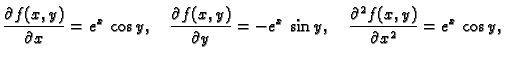
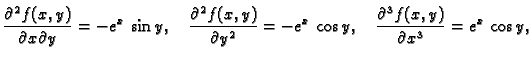
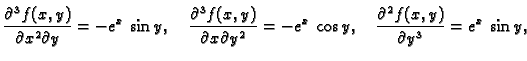
![]()
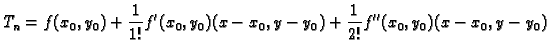
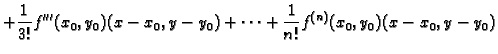
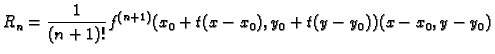
![]() u točki
u točki
![]() pomoću polinoma od dvije varijable
pomoću polinoma od dvije varijable ![]() Greška te aproksimacije je
Greška te aproksimacije je ![]()
![]() u okolini točke
u okolini točke ![]() Polinomi
Polinomi ![]() nisu
ucrtani, jer je
nisu
ucrtani, jer je ![]() i
i ![]()
![]() Radi jednostavnosti
pokažimo da to vrijedi za Taylorov polinom drugog stupnja.
Radi jednostavnosti
pokažimo da to vrijedi za Taylorov polinom drugog stupnja.
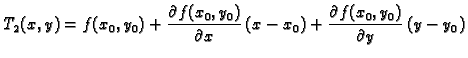
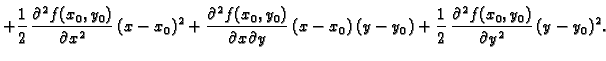
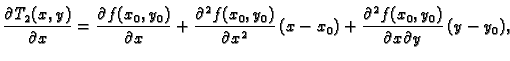
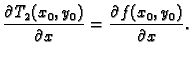
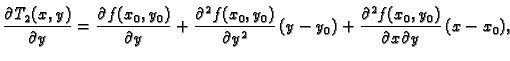
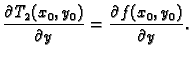
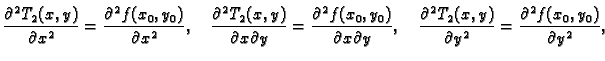
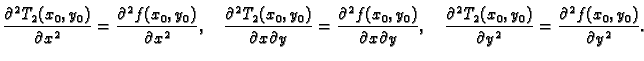
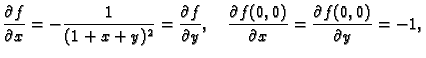
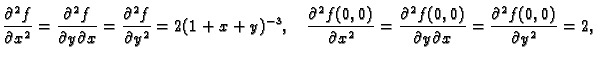
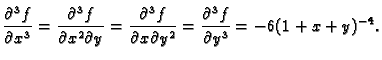
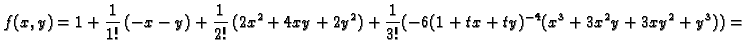
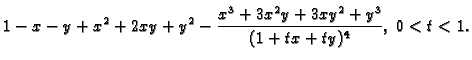
![]() klase
klase
![]() U tom slučaju imamo Taylorovu
formulu za bilo koji
U tom slučaju imamo Taylorovu
formulu za bilo koji ![]() Ako je pri tom još
Ako je pri tom još
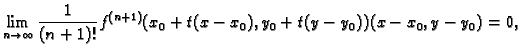
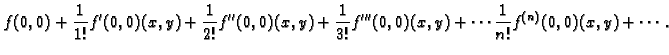
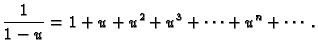
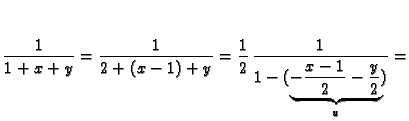
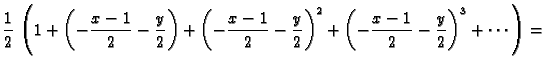
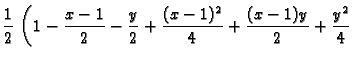
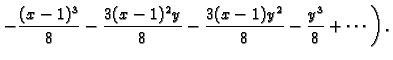
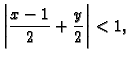
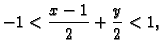
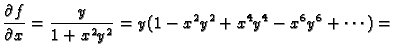
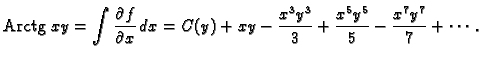
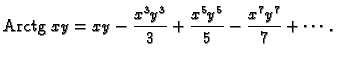
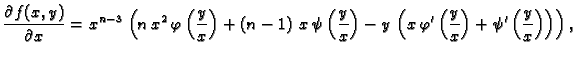
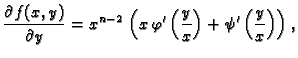
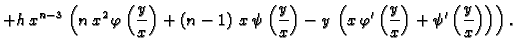
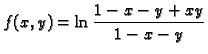
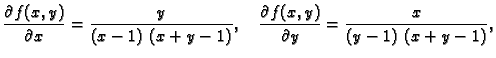
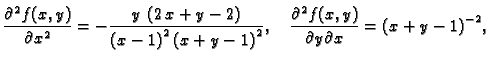
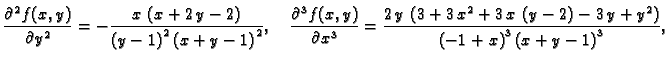
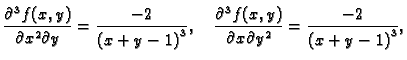
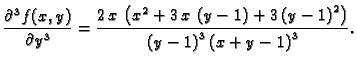
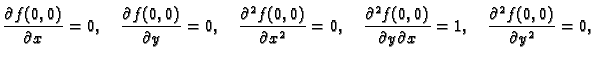
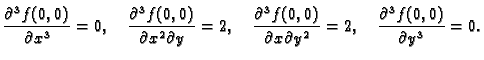
![]() imamo
imamo