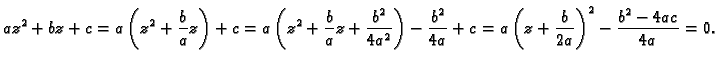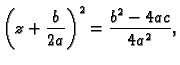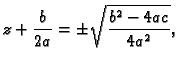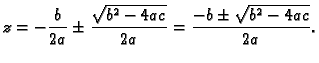



Next: Supremum i infimum
Up: Dodaci
Previous: Dodaci
Contents
Index
Subsections
Skup kompleksnih brojeva
Skup
gdje je 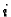 broj koji ima svojstvo
se zove skup kompleksnih brojeva.
Ako je
onda imamo sljedeće oznake.
broj koji ima svojstvo
se zove skup kompleksnih brojeva.
Ako je
onda imamo sljedeće oznake. 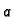 je realan dio
kompleksnog broja
je realan dio
kompleksnog broja 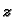 i piše se
i piše se
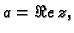
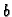 je imaginaran dio kompleksnog broja
je imaginaran dio kompleksnog broja 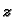 i piše se
i piše se
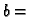 Im
Im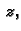
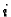 je imaginarna jedinica.
je imaginarna jedinica.
Broj
se zove kompleksno konjugiran broju
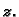
Neka je
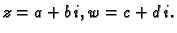
Lako se provjeri da su ovako definirani zbrajanje i množenje komutativni,
tj. da vrijedi
asocijativni, tj. da vrijedi
i da je množenje distributivno u odnosu na zbrajanje, tj. da vrijedi
Kompleksni broj je jednak nuli samo ako je 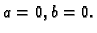 Svaki od nule
različit kompleksni broj ima sebi recipročan, tj. ako je
Svaki od nule
različit kompleksni broj ima sebi recipročan, tj. ako je
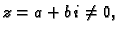 onda postoji
onda postoji
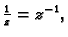 i pri tom je
Također vrijedi
i pri tom je
Također vrijedi
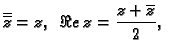
Im
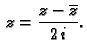
Modul kompleksnog broja je realan
broj
U odnosu na operacije, modul ima sljedeća svojstva.
Dokažimo da vrijedi
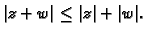 Uočimo
najprije da je
Uočimo
najprije da je
Sada imamo
Nakon vađenja drugog korijena, zbog pozitivnosti brojeva 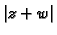 i
i
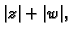 slijedi
slijedi
Svaki kompleksni broj je potpuno zadan s dva realna broja, i pri tom je
važno koji je prvi (realni dio) a koji drugi (imaginarni dio). Obratno,
svakom uređenom paru realnih brojeva 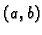 možemo pridružiti
kompleksni broj
možemo pridružiti
kompleksni broj 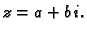 Tako je dano obostrano jednoznačno
pridruživanje između skupova
Tako je dano obostrano jednoznačno
pridruživanje između skupova 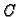 i
i 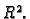 To ipak ne znači da su to isti
skupovi. U
To ipak ne znači da su to isti
skupovi. U 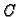 imamo operacije zbrajanja i množenja tj. znamo računati,
a u
imamo operacije zbrajanja i množenja tj. znamo računati,
a u 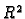 nemamo nikakve operacije. Elemente iz
nemamo nikakve operacije. Elemente iz 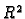 možemo crtati kao
točke u ravnini. Obostrano jednoznačno pridruživanje između
možemo crtati kao
točke u ravnini. Obostrano jednoznačno pridruživanje između 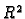 i
i 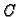 omogućava da se i kompleksni brojevi crtaju u ravnini kao točke. Razlika
između ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine
u kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj točke
možemo zbrajati i množiti, pa zato ova druga ima posebno ime. Ona se zove
Gaussova ravnina ili kompleksna ravnina.
omogućava da se i kompleksni brojevi crtaju u ravnini kao točke. Razlika
između ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine
u kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj točke
možemo zbrajati i množiti, pa zato ova druga ima posebno ime. Ona se zove
Gaussova ravnina ili kompleksna ravnina.
Zbrajanje i odbijanje točaka u Gaussovoj ravnini se vrši po pravilu
paralelograma kao na slici.
Neka je
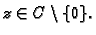 Broju
Broju 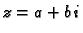 pripada u kompleksnoj
ravnini točka
pripada u kompleksnoj
ravnini točka 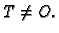 Toj točki pripada u polarnom koordinatnom
sustavu uređen par brojeva
Toj točki pripada u polarnom koordinatnom
sustavu uređen par brojeva
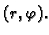 Pri tom je
Pri tom je
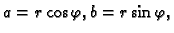 a
a
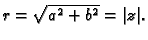 Tako je
Tako je
Zapis
se zove trigonometrijski oblik
kompleksnog broja. Broj 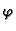 se zove argument
broja
se zove argument
broja 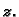 Broju
Broju 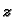 je pridruženo beskonačno mnogo vrijednosti
argumenta,
je pridruženo beskonačno mnogo vrijednosti
argumenta,
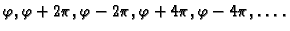 Vrijednost koja se nalazi u
Vrijednost koja se nalazi u
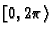 se zove glavna vrijednost argumenta.
se zove glavna vrijednost argumenta.
Trigonometrijski oblik kompleksnog broja je pogodan za operacije množenja,
dijeljenja, potenciranja i korjenovanja kompleksnih brojeva.
Neka su
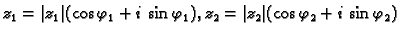 dva kompleksna broja.
dva kompleksna broja.
Dakle
Primjer 8.1
Što znači pomnožiti kompleksni broj
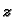
s
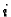
?
Rješenje. Trigonometrijski oblik imaginarne jedinice je
pa je tako
što je kompleksni broj istog modula, dakle na središnjoj kružnici
radiusa
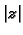
kao i
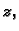
a argumenta za
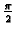
većeg nego
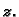
To znači da se množenje s
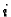
u Gaussovoj ravnini provodi rotiranjem
za kut
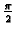
oko ishodišta u smjeru protivnom kazaljci na
satu.
Dakle
Specijalno, ako je 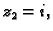 onda je
pa prema tome dijeljenje s
onda je
pa prema tome dijeljenje s 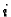 u Gaussovoj ravnini ima efekt rotacije za
kut
u Gaussovoj ravnini ima efekt rotacije za
kut
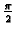 oko ishodišta u smjeru kretanja kazaljke na satu.
oko ishodišta u smjeru kretanja kazaljke na satu.
Na temelju ovih formula možemo grafički množiti i dijeliti kompleksne
brojeve u Gaussovoj ravnini.
Objašnjenje. Argument produkta jednak je zbroju
argumenata, pa se kut određuje kao zbroj
dva kuta, a modul produkta zadovoljava sljedeći razmjer
Tako se modul određuje pomoću sličnosti trokuta.
Argument kvocijenta jednak je razlici argumenata, pa se kut određuje kao
razlika dva kuta, a modul kvocijenta zadovoljava sljedeći razmjer
Tako se modul određuje pomoću sličnosti trokuta.
Iz množenja, pomoću matematičke indukcije, slijedi
za svaki prirodni broj 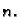
Primjer 8.2
Izračunati
Rješenje.
Dakle, za
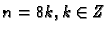
rezultat je
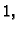
za
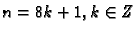
rezultat je
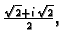
za
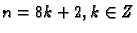
rezultat je
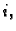
za
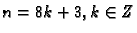
rezultat je
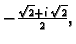
za
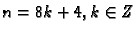
rezultat je
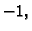
za
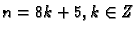
rezultat je
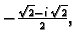
za
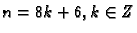
rezultat je
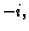
za
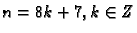
rezultat je
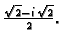
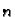 -tih korijena kompleksnog broja
-tih korijena kompleksnog broja 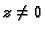 ima točno
ima točno 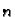 i oni su dani
ovom formulom
Modul im je svima jednak i to
i oni su dani
ovom formulom
Modul im je svima jednak i to
![$ \sqrt[n]{\vert z\vert},$](img3799.gif) pa se u Gaussovoj
ravnini nalaze na središnjoj kružnici s tim radiusom. Prvi korijen ima
argument
pa se u Gaussovoj
ravnini nalaze na središnjoj kružnici s tim radiusom. Prvi korijen ima
argument
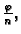 a sljedeći korijeni se dobivaju
uvećavanjem argumenta prethodnog korijena za
a sljedeći korijeni se dobivaju
uvećavanjem argumenta prethodnog korijena za
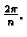 To znači
da su korijeni zapravo vrhovi određenog pravilnog
To znači
da su korijeni zapravo vrhovi određenog pravilnog 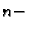 terokuta upisanog
središnjoj kružnici radiusa
terokuta upisanog
središnjoj kružnici radiusa
![$ \sqrt[n]{\vert z\vert}.$](img3803.gif)
Objašnjenje. Naći
![$ \sqrt[n]{z}=w$](img3804.gif) je isto što i
naći
je isto što i
naći 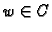 takav da je
takav da je 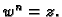 Neka je
Neka je
Pretpostavimo da je
Jednakost 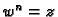 prelazi u jednakost
Odatle
Dakle za svaki
prelazi u jednakost
Odatle
Dakle za svaki 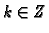 imamo po jedan
imamo po jedan 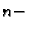 ti korijen broja
ti korijen broja 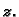 Međutim,
među njima ima jednakih. Zbog
i periodičnosti trigonometrijskih funkcija, slijedi da se korijeni
ponavljaju nakon svakih
Međutim,
među njima ima jednakih. Zbog
i periodičnosti trigonometrijskih funkcija, slijedi da se korijeni
ponavljaju nakon svakih 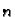 cijelih brojeva.
cijelih brojeva.
Primjer 8.3
Nađimo
![$ \sqrt[3]{-1}.$](img3814.gif)
Rješenje. Modul je 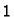 , a argument je
, a argument je 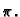 Dakle treći korijeni
su
Dakle treći korijeni
su
Na kraju dodajmo da je kod drugog korijena 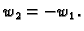
Zaista,
To ima posljedicu
da formula za rješenja kvadratne jednadžbe vrijedi i u slučaju kada su
koeficijenti u jednadžbi kompleksni brojevi.
Zaista, neka je
gdje su 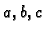 kompleksni brojevi. Rješenja gornje jednadžbe se dobiju
ovako.
Odatle
Vidimo da je formula za rješenja kvadratne jednadžbe ista, bez obzira na
to da li su koeficijenti u jednadžbi realni ili kompleksni brojevi.
kompleksni brojevi. Rješenja gornje jednadžbe se dobiju
ovako.
Odatle
Vidimo da je formula za rješenja kvadratne jednadžbe ista, bez obzira na
to da li su koeficijenti u jednadžbi realni ili kompleksni brojevi.




Next: Supremum i infimum
Up: Dodaci
Previous: Dodaci
Contents
Index
Salih Suljagic
2000-03-11
![]()
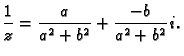
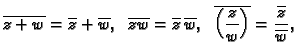
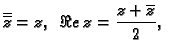 Im
Im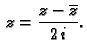
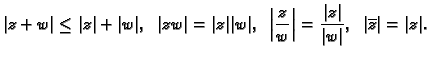
![]() Uočimo
najprije da je
Uočimo
najprije da je
![]() možemo pridružiti
kompleksni broj
možemo pridružiti
kompleksni broj ![]() Tako je dano obostrano jednoznačno
pridruživanje između skupova
Tako je dano obostrano jednoznačno
pridruživanje između skupova ![]() i
i ![]() To ipak ne znači da su to isti
skupovi. U
To ipak ne znači da su to isti
skupovi. U ![]() imamo operacije zbrajanja i množenja tj. znamo računati,
a u
imamo operacije zbrajanja i množenja tj. znamo računati,
a u ![]() nemamo nikakve operacije. Elemente iz
nemamo nikakve operacije. Elemente iz ![]() možemo crtati kao
točke u ravnini. Obostrano jednoznačno pridruživanje između
možemo crtati kao
točke u ravnini. Obostrano jednoznačno pridruživanje između ![]() i
i ![]() omogućava da se i kompleksni brojevi crtaju u ravnini kao točke. Razlika
između ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine
u kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj točke
možemo zbrajati i množiti, pa zato ova druga ima posebno ime. Ona se zove
Gaussova ravnina ili kompleksna ravnina.
omogućava da se i kompleksni brojevi crtaju u ravnini kao točke. Razlika
između ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine
u kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj točke
možemo zbrajati i množiti, pa zato ova druga ima posebno ime. Ona se zove
Gaussova ravnina ili kompleksna ravnina.
![]() Broju
Broju ![]() pripada u kompleksnoj
ravnini točka
pripada u kompleksnoj
ravnini točka ![]() Toj točki pripada u polarnom koordinatnom
sustavu uređen par brojeva
Toj točki pripada u polarnom koordinatnom
sustavu uređen par brojeva
![]() Pri tom je
Pri tom je
![]() a
a
![]() Tako je
Tako je
![]() dva kompleksna broja.
dva kompleksna broja.
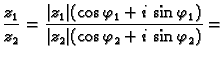
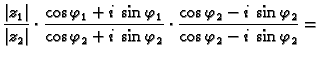
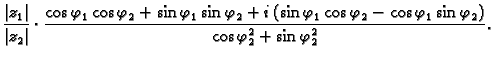
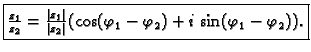
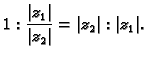
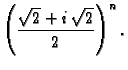
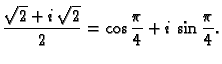
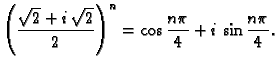
![% latex2html id marker 46511
$\displaystyle \fbox{$\sqrt[n]{z}=\sqrt[n]{\vert z\...
...rphi+2k\pi}{n}+
i\,\sin \frac{\varphi+2k\pi}{n}\right),\;\;k=0,1,\ldots ,n-1$.}$](img3798.gif)
![]() je isto što i
naći
je isto što i
naći ![]() takav da je
takav da je ![]() Neka je
Neka je
![$\displaystyle \vert w\vert=\sqrt[n]{\vert z\vert},\hspace{1cm}
\psi=\frac{\varphi+2k\pi}{n}=\frac{\varphi}{n}+\frac{2k\pi}{n},\;k\in Z.$](img3811.gif)
![]() , a argument je
, a argument je ![]() Dakle treći korijeni
su
Dakle treći korijeni
su
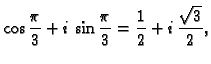
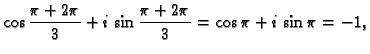
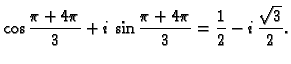
![]()