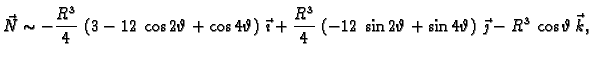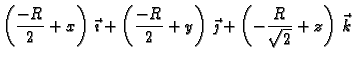



Next: Polja
Up: Krivulje i krivuljni integrali
Previous: Krivuljni integral 2. vrste
Contents
Index
Subsections
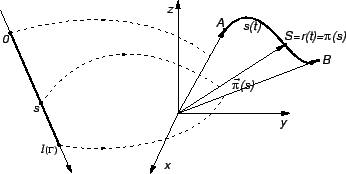
Krivulju 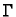 možemo parametrizirati tako da za segment uzmemo
možemo parametrizirati tako da za segment uzmemo
![$ [0,\ell(\Gamma)],$](img1990.gif) gdje je
gdje je
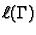 duljina krivulje
duljina krivulje 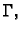 a za parametar duljinu luka od jedne rubne točke. Neka je
a za parametar duljinu luka od jedne rubne točke. Neka je 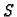 ona
točka na krivulji, za koju je duljina luka
ona
točka na krivulji, za koju je duljina luka
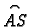 upravo jednaka
upravo jednaka 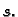 Tada stavimo
Tada stavimo
![$ S=\pi(s),\;\;s\in [0,\ell(\Gamma)].$](img1994.gif) Dakle,
Dakle, 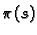 je ona točka na krivulji, čija je `udaljenost' od
točke
je ona točka na krivulji, čija je `udaljenost' od
točke 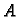 (početne točke) po luku
krivulje jednaka
(početne točke) po luku
krivulje jednaka 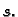
Definicija 29
Parametrizacija
![$ ([0,\ell(\Gamma)],\vec{\pi})$](img1996.gif)
krivulje
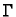
se zove
prirodna
parametrizacija.
Nađimo vezu između parametrizacije ![$ ([a,b],r)$](img1998.gif) i prirodne parametrizacije
i prirodne parametrizacije
![$ ([0,\ell(\Gamma)],\pi).$](img1999.gif)
Iz formule za duljinu luka krivulje slijedi da je
duljina luka od točke
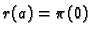 do točke
do točke
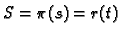 dana formulom
dana formulom
tako da je
Iz ove druge formule slijedi
Dakle,
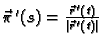 i to
je jedinični vektor u smjeru tangente.
i to
je jedinični vektor u smjeru tangente.
Definicija 30
Vektor
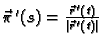
se
zove
jedinični vektor tangente i označava s
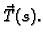
Primjer 3.18
Nađimo prirodnu parametrizaciju luka kružnice radiusa
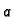
u prvom kvadrantu.
Rješenje.
pa je
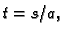
i prirodna parametrizacija je
Primjer 3.19
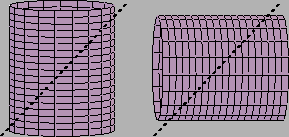
Kako treba izrezati dva jednaka pravokutna lima na jednom
rubu, da bi savijeni u valjke i spojeni činili oluk pod
pravim kutem?
Rješenje. Dovoljno je riješiti problem za jedan lim. Neka
stranica koju želimo rezati ima duljinu 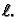 Poprečni presjek
takvog lima nakon savijanja u valjak je kružnica polumjera
Poprečni presjek
takvog lima nakon savijanja u valjak je kružnica polumjera
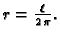 Pretpostavimo da je jedan valjak postavljen
tako da mu je os simetrije os
Pretpostavimo da je jedan valjak postavljen
tako da mu je os simetrije os 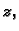 a drugi tako da mu je os simetrije
os
a drugi tako da mu je os simetrije
os 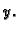 Ako se sijeku pod pravim kutem, onda se presjek nalazi u
ravnini čija jednadžba je
Ako se sijeku pod pravim kutem, onda se presjek nalazi u
ravnini čija jednadžba je 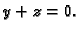 Tako je krivulja presjeka dana
kao presjek dvije plohe, i to
Tako je krivulja presjeka dana
kao presjek dvije plohe, i to
Da bismo našli kako treba rezati lim, treba poprečni presjek
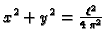
parametrizirati prirodno i zatim
ustanoviti kako
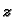
ovisi o prirodnom parametru. Prirodna
parametrizacija je
Iz formule za
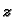
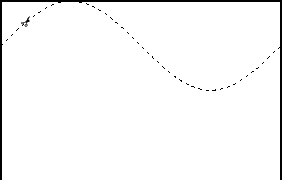
se vidi da lim treba rezati tako da gornji rub
predstavlja sinusoidu, čiji je period
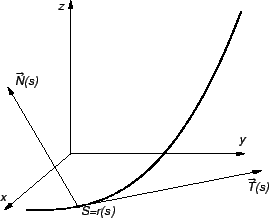
Vektorska funkcija
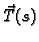 ima jedinične vektore kao slike, pa je
ima jedinične vektore kao slike, pa je
i odatle
Tako je vektor
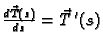 okomit na
okomit na
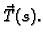
Definicija 31
Vektor
zovemo
jediničnim vektorom normale,
a broj
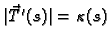 zakrivljenoš3u
zakrivljenoš3u krivulje u točki
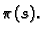
Broj
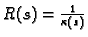
zovemo
radiusom
zakrivljenosti
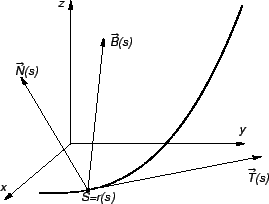
Za proizvoljnu vrijednost prirodnog parametra 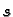 definiramo
definiramo
Budući da su vektori
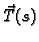 i
i
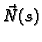 jedinični i međusobno
okomiti, vektor
jedinični i međusobno
okomiti, vektor
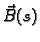 je jediničan, i okomit na
je jediničan, i okomit na
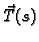 i
i
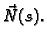
Definicija 32
Vektor
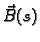
zovemo
jediničnim vektorom
binormale.
Vektori
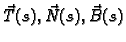 čine desnu ortonormiranu bazu u svakoj točki krivulje, no kako
idemo po krivulji, ona rotira.
čine desnu ortonormiranu bazu u svakoj točki krivulje, no kako
idemo po krivulji, ona rotira.
Kao i ranije zaključujemo da je
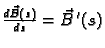 okomit na
okomit na
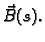 Zatim,
Zatim,
Odatle izlazi da je
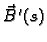 okomit i na
okomit i na
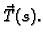 Tako je
Tako je
Definicija 33
Broj
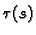
zovemo
torzijom krivulje u točki
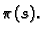
Prirodna parametrizacija ima značajnu teorijsku važnost, no u praktičnom
računanju može biti komplicirano s njom računati. Zato su nam važne
formule, koje koriste bilo koju parametrizaciju. Tako se za zakrivljenost
može izvesti formula
Doista, iz
slijedi
odnosno
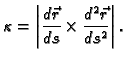 |
(3.1) |
Ako je krivulja parametrizirana nekim parametrom 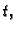 onda je
Odatle
No,
Ako ovo uvrstimo u (3.1), dobivamo upravo formulu za
zakrivljenost pomoću proizvoljnog parametra.
onda je
Odatle
No,
Ako ovo uvrstimo u (3.1), dobivamo upravo formulu za
zakrivljenost pomoću proizvoljnog parametra.
Na sličan način se može izvesti formula za torziju
Primjer 3.20
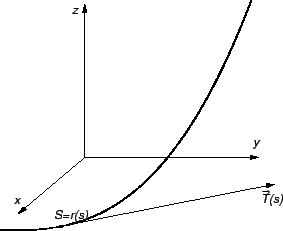
Naći zakrivljenost ravninske krivulje koja je graf funkcije
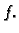
Rješenje. Za parametar možemo uzeti 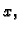 pa imamo (v. sliku 3.2.3)
pa imamo (v. sliku 3.2.3)
Odatle
pa je formula za zakrivljenost
Primjer 3.21
Naći zakrivljenost helikoide.
Rješenje.
pa je
Primjer 3.22
Brzina i akceleracija duž prostorne krivulje.
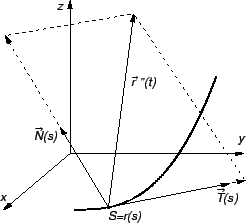
Rješenje. Ako se po krivulji giba materijalna točka, i
parametar 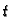 predstavlja vrijeme, onda je brzina
predstavlja vrijeme, onda je brzina
Vektor
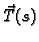
je jediničan i on daje smjer brzine, dok je
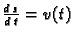
iznos brzine.
Akceleracija je derivacija brzine, pa je
Dakle, akceleracija se rastavlja na komponentu u smjeru tangente
koja predstavlja linijsku akceleraciju, i na komponentu u smjeru
normale
gdje je
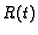
radius zakrivljenosti. To je ustvari centripetalna
akceleracija, koja u slučaju jednolikog gibanja po kružnici iznosi
jer je u tom slučaju
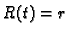
radius kružnice, a
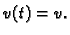
Primjer 3.23
Naći torziju helikoide.
Rješenje.
pa je tako
Primjer 3.24
Torzija ravninske krivulje je 0.
Rješenje. Doista,
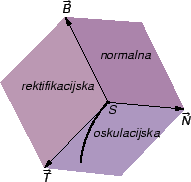
Bilo da želimo naći vektore
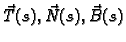 ili
jednadžbe ovih ravnina, dovoljno je naći vektore u smjeru vektora
trobrida pratioca, jer je nakon toga lako normirati ih.
ili
jednadžbe ovih ravnina, dovoljno je naći vektore u smjeru vektora
trobrida pratioca, jer je nakon toga lako normirati ih.
a)
pa je
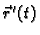 vektor u smjeru vektora
vektor u smjeru vektora
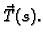
b) Zatim
Dakle
Tako je
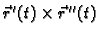 vektor u smjeru vektora
vektor u smjeru vektora
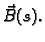
c) Konačno,
pa je
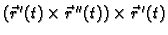 vektor u smjeru vektora
vektor u smjeru vektora
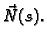
Primjer 3.25
Naći normalnu, rektifikacijsku i oskulacijsku ravninu na
helikoidu u točki
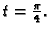
Rješenje.
a)
pa je jednadžba normalne ravnine
b)
pa je jednadžba oskulacijske ravnine
c)
pa je jednadžba rektifikacijske ravnine
- 1.
- Objasnite pojam parametrizacija krivulje. Koju parametrizaciju
zovemo prirodnom?
- 2.
- Kako se definiraju zakrivljenost i torzija glatke krivulje? Kojim
formulama se računaju?
- 3.
- Što je trobrid pratilac?
- 4.
- Definirajte oskulacijsku, normalnu i rektifikacijsku ravninu. Kako
se mogu naći njihove jednadžbe?
- 1.
- Što predstavlja helikoida kad se valjak, na koji je
namotana razreže po jednoj izvodnici i izravna?
Rješenje. Parametrizacija helikoide je
Da bismo riješili zadatak, treba prijeći na prirodni parametar
poprečnog presjeka
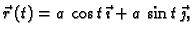 i ustanoviti kako
i ustanoviti kako 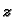 ovisi o njemu. Lako se
izračuna da je
ovisi o njemu. Lako se
izračuna da je 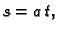 pa je parametrizacija helikoide tim
parametrom
Odatle imamo
tj. helikoida, kad se razmota, postaje pravac s koeficijentom smjera
pa je parametrizacija helikoide tim
parametrom
Odatle imamo
tj. helikoida, kad se razmota, postaje pravac s koeficijentom smjera
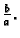
- 2.
- Prirodno parametrizirati prvi zavoj helikoide.
Rješenje. Koristeći parametrizaciju iz zadatka 1 imamo
Odatle
Tako je prirodna parametrizacija prvog zavoja helikoide
- 3.
- Naći oskulacijsku, normalnu i rektifikacijsku ravninu
Vivianijeve krivulje u točki
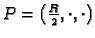 .
.
Rješenje. Parametrizacija Vivianijeve krivulje glasi (v. zadatak
2)
Iz
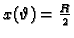 slijedi
slijedi
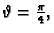 pa
je
pa
je
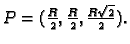
Imamo
pa je
Skalarni produkti ovih vektora, uzetih u točki
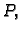 s vektorom
izjednačeni s nulom
daju tražene ravnine. Tako je jednadžba oskulacijske ravnine
normalne ravnine
rektifikacijske ravnine
s vektorom
izjednačeni s nulom
daju tražene ravnine. Tako je jednadžba oskulacijske ravnine
normalne ravnine
rektifikacijske ravnine

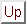



Next: Polja
Up: Krivulje i krivuljni integrali
Previous: Krivuljni integral 2. vrste
Contents
Index
Salih Suljagic
2000-03-11
![]() možemo parametrizirati tako da za segment uzmemo
možemo parametrizirati tako da za segment uzmemo
![]() gdje je
gdje je
![]() duljina krivulje
duljina krivulje ![]() a za parametar duljinu luka od jedne rubne točke. Neka je
a za parametar duljinu luka od jedne rubne točke. Neka je ![]() ona
točka na krivulji, za koju je duljina luka
ona
točka na krivulji, za koju je duljina luka
![]() upravo jednaka
upravo jednaka ![]() Tada stavimo
Tada stavimo
![]() Dakle,
Dakle, ![]() je ona točka na krivulji, čija je `udaljenost' od
točke
je ona točka na krivulji, čija je `udaljenost' od
točke ![]() (početne točke) po luku
krivulje jednaka
(početne točke) po luku
krivulje jednaka ![]()
![]() i prirodne parametrizacije
i prirodne parametrizacije
![]()
![]() do točke
do točke
![]() dana formulom
dana formulom
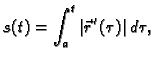
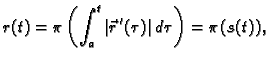
![\begin{displaymath}
% latex2html id marker 40334\begin{cases}
x(t) = a\,\cos t, & \\
y(t) = a\,\sin t, &
\end{cases}\qquad t\in [0,\pi/2],
\end{displaymath}](img2009.gif)
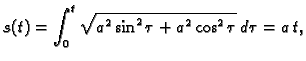
![\begin{displaymath}
% latex2html id marker 40340\begin{cases}
x(s) = a\,\cos ...
... = a\,\sin \frac{s}{a}, &
\end{cases}\qquad s\in [0,a\,\pi/2].
\end{displaymath}](img2012.gif)
![]() Poprečni presjek
takvog lima nakon savijanja u valjak je kružnica polumjera
Poprečni presjek
takvog lima nakon savijanja u valjak je kružnica polumjera
![]() Pretpostavimo da je jedan valjak postavljen
tako da mu je os simetrije os
Pretpostavimo da je jedan valjak postavljen
tako da mu je os simetrije os ![]() a drugi tako da mu je os simetrije
os
a drugi tako da mu je os simetrije
os ![]() Ako se sijeku pod pravim kutem, onda se presjek nalazi u
ravnini čija jednadžba je
Ako se sijeku pod pravim kutem, onda se presjek nalazi u
ravnini čija jednadžba je ![]() Tako je krivulja presjeka dana
kao presjek dvije plohe, i to
Tako je krivulja presjeka dana
kao presjek dvije plohe, i to
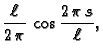
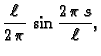
![$\displaystyle -y=-\frac{\ell}{2\,\pi}\,\sin \frac{2\,\pi\,s}{\ell},
\hspace{2cm} s\in [0,\ell].$](img2027.gif)
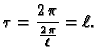
![]() ima jedinične vektore kao slike, pa je
ima jedinične vektore kao slike, pa je
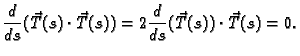
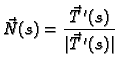
![]() definiramo
definiramo
![]() čine desnu ortonormiranu bazu u svakoj točki krivulje, no kako
idemo po krivulji, ona rotira.
čine desnu ortonormiranu bazu u svakoj točki krivulje, no kako
idemo po krivulji, ona rotira.
![]() okomit na
okomit na
![]() Zatim,
Zatim,
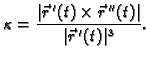
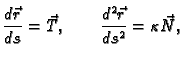
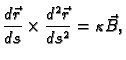
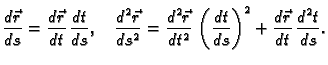
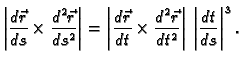
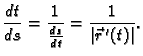
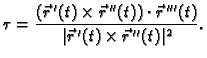
![]() pa imamo (v. sliku 3.2.3)
pa imamo (v. sliku 3.2.3)
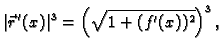
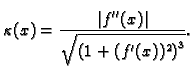
![]() predstavlja vrijeme, onda je brzina
predstavlja vrijeme, onda je brzina
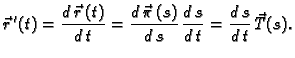
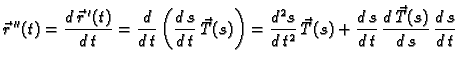
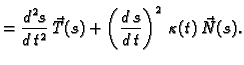
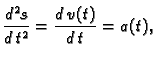
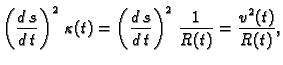
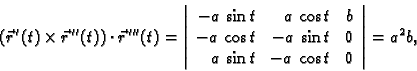
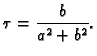
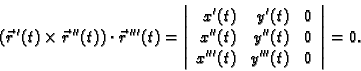
![]() ili
jednadžbe ovih ravnina, dovoljno je naći vektore u smjeru vektora
trobrida pratioca, jer je nakon toga lako normirati ih.
ili
jednadžbe ovih ravnina, dovoljno je naći vektore u smjeru vektora
trobrida pratioca, jer je nakon toga lako normirati ih.
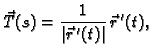
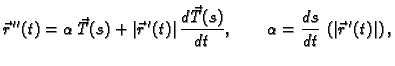
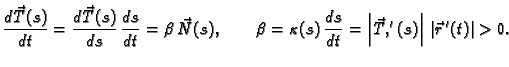
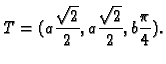
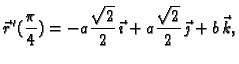
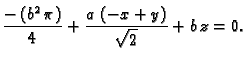
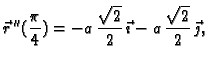
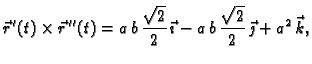
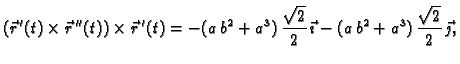
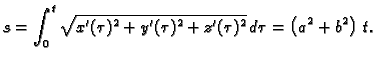
![\begin{displaymath}
% latex2html id marker 40626\begin{cases}
\displaystyle x(...
...&
\end{cases}\qquad s\in [0,2\left( {a^2} + {b^2} \right)\pi].
\end{displaymath}](img2113.gif)
![\begin{displaymath}
% latex2html id marker 40630\begin{cases}
x(\vartheta)=R\...
...rtheta, &
\end{cases} \qquad \vartheta{}\in [0,\frac{\pi}{2}].
\end{displaymath}](img2115.gif)