- 1.
- Ako funkcija raste na
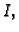 onda je
onda je
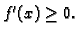 Obratno, ako je
Obratno, ako je
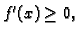 onda funkcija raste.
onda funkcija raste.
- 2.
- Ako funkcija pada na
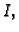 onda je
onda je
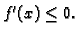 Obratno, ako je
Obratno, ako je
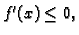 onda funkcija pada.
onda funkcija pada.
Dokaz. Dokažimo prvu tvrdnju.
1. Neka ![]() raste na
raste na ![]() Pretpostavimo, suprotno tvrdnji, da je
Pretpostavimo, suprotno tvrdnji, da je ![]() za neki
za neki ![]() To znači da za neki
To znači da za neki ![]() vrijedi
vrijedi
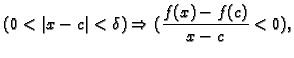
2. Obratno, neka je
![]() za svaki
za svaki ![]() Neka su
Neka su
![]() proizvoljni, i neka je
proizvoljni, i neka je ![]() Tada po Lagrangeovom teoremu
Tada po Lagrangeovom teoremu