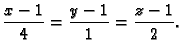



Next: Krivuljni integral 1. vrste
Up: Krivulje i krivuljni integrali
Previous: Krivulje i krivuljni integrali
Contents
Index
Subsections
Podsjetimo se da
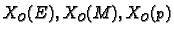 predstavlja vektorski prostor
svih radijvektora s početkom u
predstavlja vektorski prostor
svih radijvektora s početkom u 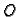 u prostoru
u prostoru 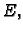 ravnini
ravnini  na
pravcu
na
pravcu 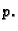 (v. 8.3)
(v. 8.3)
Definicija 21
Neka je
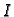
interval u
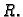
Funkciju
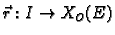
zovemo
vektorskom funkcijom jedne (realne)
varijable.
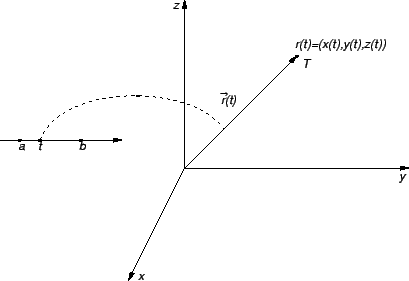
U Kartezijevom pravokutnom koordinatnom sustavu u prostoru možemo pisati
Tako su jednom vektorskom funkcijom zadane tri
skalarne funkcije  One se zovu skalarne
komponente vektorske
funkcije
One se zovu skalarne
komponente vektorske
funkcije 
Obzirom na identifikaciju radijvektora, njegovog vrha i uređene
trojke realnih brojeva, uz funkciju 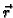 možemo promatrati i
funkciju
možemo promatrati i
funkciju
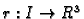
Primjer 3.1
Vektorska funkcija
je konstanta. Ma kakav bio
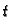
njezina vrijednost je uvijek vektor
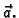
Primjer 3.2
Vektorska funkcija
je zapravo na drugi način napisana funkcija
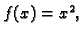
jer je
tj.
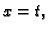
a
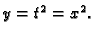
Primjer 3.3
Vektorska funkcija
ima kao vrijednosti radijvektore, čiji vrhovi opisuju spiralu u
prostoru.
Definicija 22
Neka je
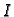
interval u
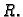
Za funkciju
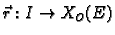
kažemo da je
neprekidna u točki 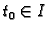
ako
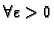
postoji
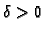
tako da
Ako je funkcija
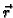
neprekidna u svakoj točki iz
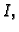
onda
kažemo da je
neprekidna na 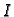
. U protivnom kažemo da ima
prekid na 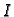
.
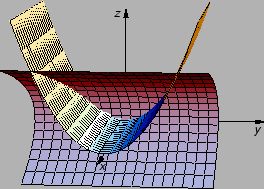
Figure 3.1:
Neprekidna i prekidna vektorska funkcija.
|
|
Podsjetimo se
pa iz
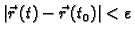 slijedi
To znači da neprekidnost vektorske funkcije povlači neprekidnost
svake od njezinih skalarnih komponenti.
slijedi
To znači da neprekidnost vektorske funkcije povlači neprekidnost
svake od njezinih skalarnih komponenti.
Obratno, ako su funkcije  neprekidne u
neprekidne u 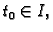 onda
onda
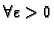 postoje
postoje
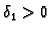 takav da je
takav da je
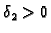 takav da je
takav da je
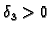 takav da je
Za
takav da je
Za
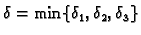 vrijede sve tri
nejednakosti, pa je
To pokazuje da iz neprekidnosti skalarnih komponenti slijedi
neprekidnost vektorske funkcije.
vrijede sve tri
nejednakosti, pa je
To pokazuje da iz neprekidnosti skalarnih komponenti slijedi
neprekidnost vektorske funkcije.
Navedimo sada bez dokaza neka svojstva neprekidnih vektorskih
funkcija.
Definicija 23
Neka je
![$ [a,b]$](img986.gif)
segment u
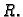
Za funkciju
![$ \vec{r}:[a,b]\rightarrow
X_O(E)$](img1650.gif)
kažemo da je
neprekidna na segmentu ![$ [a,b],$](img1000.gif)
ako postoji interval
![$ I\supset [a,b]$](img1651.gif)
i neprekidna vektorska funkcija
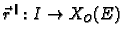
tako da je
![$ \vec{r}\,(t)=
\vec{r}^{\,\sharp}(t),\;\forall t\in [a,b].$](img1653.gif)
Definicija 24
Neka je
![$ \vec{r}:[a,b]\rightarrow
X_O(E)$](img1650.gif)
neprekidna na segmentu
![$ [a,b],$](img1000.gif)
i neka je
Skup točaka u prostoru
se zove
krivulja u prostoru.
Neka je
![$ \vec{r}:[a,b]\rightarrow
X_O(M)$](img1656.gif) neprekidna na segmentu
neprekidna na segmentu ![$ [a,b],$](img1000.gif) i neka je
i neka je
Skup točaka u prostoru
se zove
krivulja u ravnini.
Uređeni par
![$ ([a,b],\vec{r}\,)$](img1659.gif) segmenta
segmenta ![$ [a,b]$](img986.gif) i vektorske funkcije
i vektorske funkcije
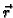 se zove parametrizacija krivulje
se zove parametrizacija krivulje 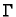 .
.
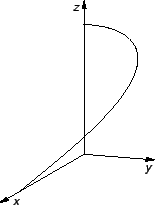
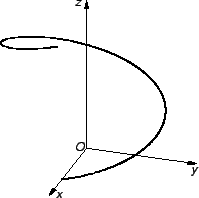
Primjer 3.4
Helikoida je krivulja parametarski zadana s
ili
Ovo je zapravo jedan zavoj helikoide. Drugu parametrizaciju možemo dobiti,
ako
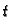
zamijenimo s
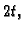
a segment s
![$ [0,\pi].$](img1665.gif)
Definicija 25
Neka je
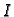
interval u
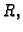
i neka je
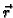
vektorska funkcija
definirana na
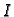
osim možda u točki
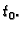
Kažemo da
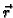
ima
limes 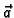 u točki
u točki 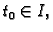
ako
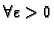
postoji
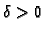
tako da
U tom slučaju pišemo
Dokaz. i) Ako je 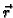 neprekidna u točki
neprekidna u točki 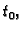 onda
onda
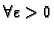 postoji
postoji 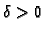 tako da
tako da
pa pogotovo
Odatle slijedi da 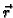 ima limes u točki
ima limes u točki 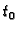 i
i
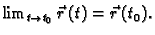
ii) Neka 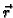 ima limes u točki
ima limes u točki 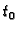 i neka je
i neka je
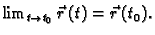 To znači da
To znači da
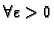 postoji
postoji 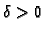 tako da
tako da
Specijalno za
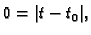 tj. za
tj. za 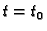 je
je
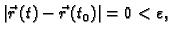 pa slijedi
tj. funkcija je neprekidna u točki
pa slijedi
tj. funkcija je neprekidna u točki 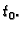
Teorem 16
Neka funkcije
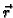
i
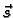
imaju limese u točki
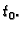
Tada
- 1.
-
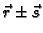 ima limes u točki
ima limes u točki 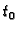 i
i
- 2.
- za
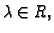
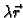 ima limes u točki
ima limes u točki 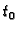 i
i
- 3.
- za konstantan
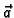 funkcija
funkcija
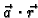 ima
limes u točki
ima
limes u točki 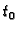 i
i
- 4.
-
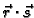 ima limes u točki
ima limes u točki 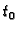 i
i
- 5.
-
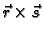 ima limes u točki
ima limes u točki 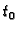 i
i
Dokaz.
Definicija 26
Neka je
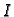
interval u
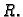
Za funkciju
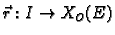
kažemo da je
derivabilna u
točki 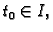
ako postoji vektor
i taj vektor zovemo
derivacijom funkcije 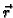 u
točki
u
točki 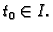
Kažemo da 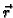 ima derivaciju, u oznaci
ima derivaciju, u oznaci
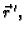 ako je derivabilna u svakoj točki, i pri tom
ako je derivabilna u svakoj točki, i pri tom
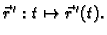
Teorem 17
Neka funkcije
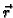
i
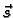
imaju derivacije u točki
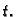
Tada
- 1.
-
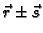 ima derivaciju u točki
ima derivaciju u točki 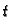 i
i
- 2.
-
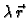 ima derivaciju u točki
ima derivaciju u točki 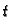 i
i
- 3.
-
 ima derivaciju u točki
ima derivaciju u točki 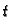 i
i
- 4.
-
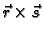 ima derivaciju u točki
ima derivaciju u točki 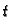 i
i
Dokaz.
Krivulja u ravnini može poprimiti i ovako neobične oblike kao na
sljedećim slikama.
Nastavljajući kao u ovom nizu mogli bismo točkama krivulje ispuniti
cijeli kvadrat. Naravno, skup točaka koje ispunjavaju kvadrat u
ravnini ne možemo smatrati krivuljom u uobičajenom smislu. Da
izbjegnemo takve slučajeve, moramo na funkciju 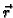 naložiti još neke uvjete. Tako imamo sljedeću definiciju.
naložiti još neke uvjete. Tako imamo sljedeću definiciju.
Definicija 27
Za krivulju
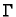
s parametrizacijom
![$ ([a,b],\vec{r}\,)$](img1659.gif)
kažemo
da je
Jordanov luk ili
jednostavna glatka krivulja,
ako vrijedi
- 1.
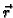 je injekcija, tj.
je injekcija, tj.
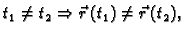
- 2.
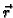 je funkcija klase
je funkcija klase
![$ C^1([a,b]),$](img1519.gif) tj. ima neprekidnu
prvu derivaciju,
tj. ima neprekidnu
prvu derivaciju,
- 3.
-
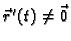 za svaki
za svaki
![$ t\in [a,b].$](img1702.gif)
Za krivulju
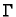
s parametrizacijom
![$ ([a,b],\vec{r}\,)$](img1659.gif)
kažemo
da je
zatvoren Jordanov luk ili
zatvorena jednostavna glatka krivulja,
ako vrijede ova tri svojstva s jedinom iznimkom da je
Za krivulju 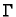 s parametrizacijom
s parametrizacijom
![$ ([a,b],\vec{r}\,)$](img1659.gif) kažemo da
je po dijelovima Jordanov luk ili po dijelovima
jednostavna glatka krivulja, ako se
segment
kažemo da
je po dijelovima Jordanov luk ili po dijelovima
jednostavna glatka krivulja, ako se
segment ![$ [a,b]$](img986.gif) može podijeliti na konačno mnogo podsegmenata
točkama
može podijeliti na konačno mnogo podsegmenata
točkama
tako, da je svaka od krivulja
![$ ([t_{i-1},t_i],\vec{r}\,),$](img1705.gif)
za
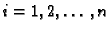
jednostavna glatka krivulja.
Figure 3.2:
a) Jednostavna glatka krivulja. b) Zatvorena jednostavna glatka krivulja. c) Po dijelovima jednostavna glatka krivulja.
|
|
Primjer 3.5
Helikoida je Jordanov luk.
Rješenje. Zaista
- 1.
-
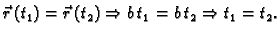
- 2.
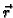 je očito klase
je očito klase
![$ C^1([0,2\pi]).$](img1709.gif)
- 3.
-
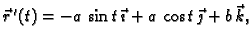 pa je
pa je
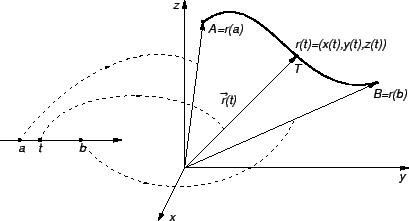
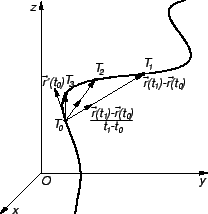
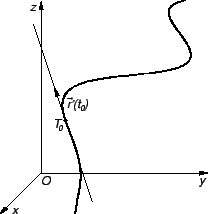
Uočimo dvije točke
 i
i
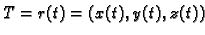 na krivulji
na krivulji  Njima su određeni vektori
Njima su određeni vektori
Vektor
 je vektor one sekante krivulje,
koja prolazi točkama
je vektor one sekante krivulje,
koja prolazi točkama  i
i 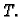 Uočimo
i pustimo da točka
Uočimo
i pustimo da točka 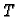 ide prema
ide prema 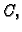 tj. da
tj. da 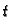 teži prema
teži prema 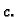 Pretpostavimo da je krivulja
Pretpostavimo da je krivulja 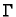 Jordanov luk. U tom slučaju postoje
pa prema tome i
Tom prilikom sekanta prelazi u tangentu, i vektor
Jordanov luk. U tom slučaju postoje
pa prema tome i
Tom prilikom sekanta prelazi u tangentu, i vektor
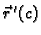 je vektor
smjera tangente na krivulju
je vektor
smjera tangente na krivulju 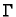 u točki
u točki 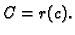 Jednadžba tangente
sada slijedi iz jednadžbe pravca kroz danu točku sa zadanim vektorom smjera.
Jednadžba tangente
sada slijedi iz jednadžbe pravca kroz danu točku sa zadanim vektorom smjera.
Primjer 3.6
Nađimo tangentu na helikoidu u točki, koja odgovara
vrijednosti parametra
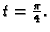
Rješenje. Točka je

pa je jednadžba tangente
Definicija 28
Za funkciju
![$ \vec{r}:[a,b]\rightarrow
X_O(E)$](img1650.gif)
kažemo da je
integrabilna na segmentu [a,b], ako
su skalarne funkcije
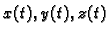
integrabilne na
![$ [a,b],$](img1000.gif)
i
tada definiramo
- 1.
-
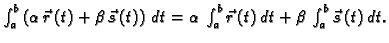
- 2.
-
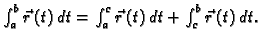
- 3.
- Ako je
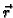 neprekidna, i
neprekidna, i 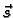 njezina
primitivna,
tj. vektorska funkcija takva da je
njezina
primitivna,
tj. vektorska funkcija takva da je
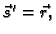 onda je
onda je
- 1.
- Objasnite pojam vektorske funkcije jedne realne varijable.
- 2.
- Kako se za takvu funkciju definiraju pojmovi neprekidnost u
točki, neprekidnost na intervalu, neprekidnost na segmentu?
- 3.
- Koja svojstva imaju neprekidne vektorske funkcije?
- 4.
- Kako se definira limes vektorske funkcije, i koja svojstva ima?
- 5.
- Definirajte derivaciju vektorske funkcije u točki, derivaciju, i
navedite njezina svojstva (pravila deriviranja).
- 6.
- Što je krivulja, a što je glatka krivulja ili Jordanov luk?
- 7.
- Kako se definira integral vektorske funkcije?
- 8.
- Koje su njegova svojstva?
- 9.
- Što je primitivna funkcija vektorske funkcije?
- 1.
- Naći jednadžbu tangente na krivulju
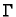 određenu kao
presjek ploha
određenu kao
presjek ploha 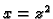 i
i 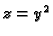 u točki s ordinatom
u točki s ordinatom 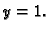
Rješenje. Krivulja se može parametrizirati tako da se za
parametar uzme 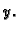 Tada je
Tada je
Točka tangiranja je 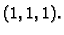 Dakle, jednadžba tangente je
Dakle, jednadžba tangente je
- 2.
- Parametrizirati Vivianijevu krivulju, tj. krivulju koja je
određena kao presjek sfere
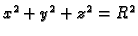 i cilindra
i cilindra
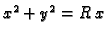 u prvom oktantu. (v. sliku 2.14.)
u prvom oktantu. (v. sliku 2.14.)
Rješenje. Budući da se krivulja nalazi na sferi, pogodno je
prijeći u sferni koordinatni sustav u prostoru.
Tako jednadžbe sfere i cilindra postaju
Kada to uvrstimo u  dobivamo
dobivamo




Next: Krivuljni integral 1. vrste
Up: Krivulje i krivuljni integrali
Previous: Krivulje i krivuljni integrali
Contents
Index
Salih Suljagic
2000-03-11
![]() predstavlja vektorski prostor
svih radijvektora s početkom u
predstavlja vektorski prostor
svih radijvektora s početkom u ![]() u prostoru
u prostoru ![]() ravnini
ravnini ![]() na
pravcu
na
pravcu ![]() (v. 8.3)
(v. 8.3)
![]() možemo promatrati i
funkciju
možemo promatrati i
funkciju
![]()
![]() neprekidne u
neprekidne u ![]() onda
onda
![]() postoje
postoje
![]() takav da je
takav da je
![]() neprekidna na segmentu
neprekidna na segmentu ![]() i neka je
i neka je
![]() segmenta
segmenta ![]() i vektorske funkcije
i vektorske funkcije
![]() se zove parametrizacija krivulje
se zove parametrizacija krivulje ![]() .
.
![]() ima limes u točki
ima limes u točki ![]() i neka je
i neka je
![]() Tada je
Tada je ![]() neprekidna u točki
neprekidna u točki ![]()
![]() neprekidna u točki
neprekidna u točki ![]() onda
onda
![]() postoji
postoji ![]() tako da
tako da
![]() ima limes u točki
ima limes u točki ![]() i neka je
i neka je
![]() To znači da
To znači da
![]() postoji
postoji ![]() tako da
tako da
![]()
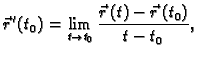
![]() ima derivaciju, u oznaci
ima derivaciju, u oznaci
![]() ako je derivabilna u svakoj točki, i pri tom
ako je derivabilna u svakoj točki, i pri tom
![]()
![]()
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,...
,...
![]() s parametrizacijom
s parametrizacijom
![]() kažemo da
je po dijelovima Jordanov luk ili po dijelovima
jednostavna glatka krivulja, ako se
segment
kažemo da
je po dijelovima Jordanov luk ili po dijelovima
jednostavna glatka krivulja, ako se
segment ![]() može podijeliti na konačno mnogo podsegmenata
točkama
može podijeliti na konačno mnogo podsegmenata
točkama
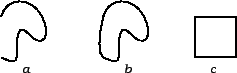
![]() i
i
![]() na krivulji
na krivulji ![]() Njima su određeni vektori
Njima su određeni vektori
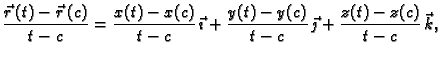
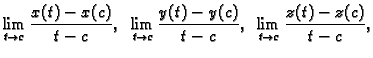
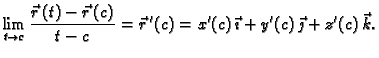
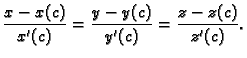
![]()
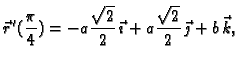
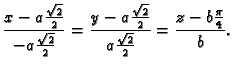

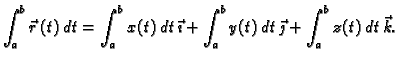
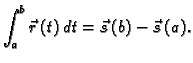
![]() Tada je
Tada je